optimization基础知识
图片来自于:《最优化:建模、算法与理论》https://bicmr.pku.edu.cn/~wenzw/optbook.html 由于《最优化:建模、算法与理论》已经很全面,因此只是将其整理一下方便查阅。 凸函数 凸函数定义 一阶条件 二阶条件 注:多元函数的泰勒展开和一元的有一些区别: 由于∇2f(x)⪰0\nabla^2f(x)\succeq 0∇2f(x)⪰0对于所有x∈domfx\in \textbf{dom} fx∈domf均成立,tx+(1−t)y∈domftx+(1-t)y\in\textbf{dom} ftx+(1−t)y∈domf,因此后面一坨大于等于0。 最优性条件 考虑 minx∈Rnf(s)(OPT)\min_{x\in\mathbb R^n} \quad f(s)\tag{OPT} x∈Rnminf(s)(OPT) 零阶最优条件 x∗=argminx∈Rnf(x)⟺f(x∗)≤f(x)∀x∈Rnx^*=\operatorname*{argmin}_{x\in\mathbb R^n}f(x)...
在Slurm集群上提交作业
配置conda环境 123module avail; # 显示当前系统中已安装的所有软件模块及其版本module load Anaconda3; # 加载 Anaconda3conda init # 初始化,只有第一次的时候需要,初始化以后要退出终端重进 之后就可以正常的配环境了,例如: 12conda create -n my_env python=3.12 -yconda install -c conda-forge numpy scipy matplotlib -y slurm脚本 一个简单的脚本 123456789101112#!/bin/bash#SBATCH --job-name=#SBATCH --nodes=#SBATCH --partition=#SBATCH --cpus-per-task=#SBATCH --gpus=#SBATCH --account=module purgemodule load Anaconda3source activate my_envpython test.py 第一行指定要使用的Unix...
最小生成树(Minimum Spanning Tree)
在一个 带权无向连通图 中,生成树(Spanning Tree)是包含图中所有顶点且边数最少的连通子图。而 最小生成树 是所有生成树中边的权重之和最小的那棵树。 Prim’s Algorithm Algorithm 思路: 初始化: 任选一个顶点作为初始子图(即生成树的起点),此时生成树包含 0条边,仅有一个顶点。 贪心扩展: 重复以下步骤,直到所有顶点都被包含在生成树中: 寻找最小边:从当前生成树的所有顶点出发,选择一条 权重最小的边,要求这条边连接生成树内的顶点(已选集合)和生成树外的顶点(未选集合)。 加入生成树:将这条边及其连接的未选顶点加入生成树,保证不形成环路。 终止条件: 当生成树包含图中所有顶点时停止(边数 = 顶点数 - 1)。 算法: 我们需要维护一个“所有点到树的最小距离”的优先队列。例如对于上图的三个灰色节点分别要储存2,8,3。 当新顶点 uuu 被加入生成树时,遍历 uuu 的所有邻接顶点 vvv,如果vvv不在树中,且u,vu,vu,v的距离比最小距离要小,则更新最小距离。由于生成树每次仅扩展一个顶点 uuu,只有 uuu...
深度优先搜索(DFS)
Algorithm 思路:当访问一个节点的邻居的时候,立即访问邻居的邻居。当一个节点的邻居都被访问完后,回溯到有邻居没有访问的节点。 Example 1234567891011121314151617181920212223242526272829303132333435363738394041class Node: def __init__(self, value): self.value = value self.color = 0 # 0-white 1-gray 2-black self.d = float('inf') self.f = float('inf') self.p = Nonenodes = {n: Node(n) for n in ['A', 'B', 'C', 'D', 'E', 'F',...
广度优先搜索(BFS)
Algorithm 思想:从点sss开始,探索所有相邻节点,一层一层探索 L0={s}L_0=\{s\}L0={s} L1L_1L1是sss的所有邻居 L2L_2L2是L1L_{1}L1中所有的点的邻居,但是不包括sss ⋯\cdots⋯ LkL_kLk是Lk−1L_{k-1}Lk−1中所有的点的邻居,但是不包括L0,⋯ ,Lk−1L_{0},\cdots,L_{k-1}L0,⋯,Lk−1中的点 color = white表示该点从未被访问过,color = gray 表示该点正在处理中,color = black表示改点已处理完 Example 12345678910111213141516171819202122232425262728293031323334353637383940class Node: def __init__(self, value): self.value = value self.color = 0 # 0-white 1-gray 2-black self.d =...
Singular Value Decomposition (SVD)
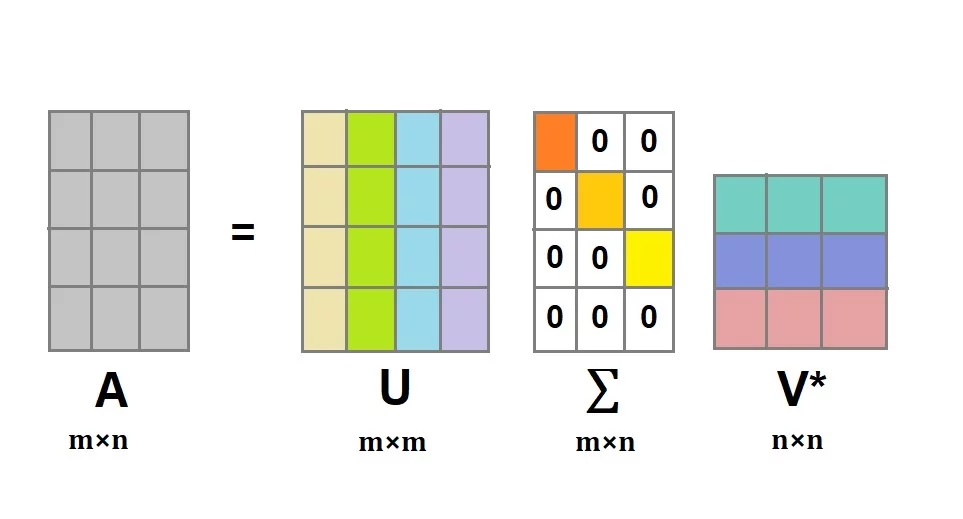
封面:Singular Value Decomposition (SVD) in Python - AskPython eigenvalue decomposition for symmetric matrix 令 A∈Rn×nA\in\mathbb R^{n\times n}A∈Rn×n 为一个对称矩阵(i.e.A⊤=AA^\top = AA⊤=A). 那么存在 A=UΛU⊤A = U\Lambda U^\top A=UΛU⊤ 其中 U=[u1,u2,⋯ ,un]∈Rn×n is orthogonalΛ=[λ1λ2⋱λn]∈Rn×n is a diagonal matrix\begin{gather*} U = [u_1,u_2,\cdots,u_n]\in\mathbb R^{n\times n} ~\text{is orthogonal}\\ \Lambda =...
Association Rule Mining
封面:Apriori Algorithm in Machine learning | by Palak Bhandari | Medium 问题定义 考虑以下表格,横轴为物品,纵轴为数据, 首先定义以下概念: item set: 一些物品的组合,例如{B,C}\{B,C\}{B,C} rule: 一个item set与另一个物品的关系,例如{B,C}→E\{B,C\}\rightarrow E{B,C}→E表示顾客购买B,CB,CB,C可以推断顾客会购买EEE support: support({B,C}→E)=∣{B,C,E}∣{\rm support}(\{B,C\}\rightarrow E)=|\{B,C,E\}|support({B,C}→E)=∣{B,C,E}∣ confidence: support({B,C}→E)/∣{B,C}∣{\rm support}(\{B,C\}\rightarrow...
QR分解
Introduction full QR A∈Rm×ns.t. m≥n, rank(A)=nA\in\mathbb R^{m\times n}\quad {\rm s.t.}~ m\geq n, ~{\rm rank}(A) = nA∈Rm×ns.t. m≥n, rank(A)=n,则存在一个分解,使得 A=QRA =QR A=QR 其中, Q∈Rm×m 是一个正交矩阵 (Q⊤Q=QQ⊤=I)R∈Rm×n 是一个上三角阵\begin{gather*} Q\in\mathbb R^{m\times m}\text{ 是一个正交矩阵 }(Q^\top Q = QQ^\top = I)\\ R\in\mathbb{R}^{m\times n}\text{ 是一个上三角阵} \end{gather*} Q∈Rm×m 是一个正交矩阵 (Q⊤Q=QQ⊤=I)R∈Rm×n 是一个上三角阵 Economic QR Q∈Rm×n 是一个 (Q⊤Q=I)R∈Rn×n 是一个上三角阵(对角线非零)\begin{gather*} Q\in\mathbb R^{m\times n}\text{ 是一个...
LU分解
封面:Epsilons, no. 3: The LU decomposition - by Tivadar Danka Definition 考虑A∈Rn×nA\in\mathbb{R}^{n\times n}A∈Rn×n,满足所有顺序主子式(leading principal minors)不为0,则存在以下分解: A=LUA = LU A=LU 其中,L∈Rn×nL\in\mathbb R^{n\times n}L∈Rn×n是一个单位下三角矩阵,U∈Rn×nU\in\mathbb{R}^{n\times n}U∈Rn×n是一个上三角阵 L=[10l1,21⋮⋮⋱ln,1ln,2⋯1]U=[u1,1⋯u1,n−1u1,n⋱⋮⋮un−1,n−1un−1,n0un,n]L = \begin{bmatrix}1&&&0\\l_{1,2}&1&&\\\vdots&\vdots&\ddots\\ l_{n,1}&l_{n,2}&\cdots&1\end{bmatrix}\quad U =...
离散傅里叶变换与快速傅里叶变换
Discrete Fourier Transform (DFT) wN=e−i2πN=cos(−2πN)+isin(−2πN)w_N = e^{-i\frac{2\pi}{N}}=\cos(-\frac{2\pi}{N})+i\sin(-\frac{2\pi}{N}) wN=e−iN2π=cos(−N2π)+isin(−N2π) FN=[111⋯11wNwN2⋯wNN−11wN2wN4⋯wN2(N−1)⋮⋮⋮⋱⋮1wNN−1wN2(N−1)⋯wN(N−1)2]=[wNjk]F_N =...