原问题

一个DRMDP（s-rec）可以表示为：

sup⁡π(⋅∣s)∈Δ(A) inf⁡Ps∑a∈Aπ(a∣s)EPs,a[R(s,a,S)+γv(S)]s.t. ∑a∈ADf(Ps,a∥P‾s,a)≤∣A∣ρPs,a∈Δ(S)for all a∈A\begin{align} \sup_{\pi(\cdot|s)\in\Delta(\mathcal{A})}~&\inf_{P_s}\sum_{a\in\mathcal{A}}\pi(a|s)\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]\\ {\rm s.t.}~ &\sum_{a\in\mathcal{A}}D_f(P_{s,a}\|\overline{P}_{s,a})\leq |\mathcal{A}|\rho\\ &P_{s,a}\in\Delta(\mathcal{S}) \quad\text{for all~} a \in \mathcal{A} \end{align}

这里我们假设R∈R∣S∣×∣A∣×∣S∣R\in\mathbb{R}^{|\mathcal{S}|\times|\mathcal{A}|\times|\mathcal{S}|}，R(st,at,st+1)R(s_t,a_t,s_{t+1})由当前时刻的状态，动作和下一时刻的状态决定。

由于目标函数对于PsP_s和π\pi都是线性的，因此可以应用Sion 极小极大定理来交换极小和极大的顺序。经过交换之后，问题转化为：

inf⁡Ps max⁡a∈AEPs,a[R(s,a,S)+γv(S)]s.t. ∑a∈ADf(Ps,a∥P‾s,a)≤∣A∣ρPs,a∈Δ(S)for all a∈A\begin{align*} \inf_{P_s}~&\max_{a\in\mathcal{A}}\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]\\ {\rm s.t.}~ &\sum_{a\in\mathcal{A}}D_f(P_{s,a}\|\overline{P}_{s,a})\leq |\mathcal{A}|\rho\\ &P_{s,a}\in\Delta(\mathcal{S}) \quad\text{for all~} a \in \mathcal{A} \end{align*}

如何理解经过极大极小定理之后随机策略变为了确定性策略：一个简单的例子

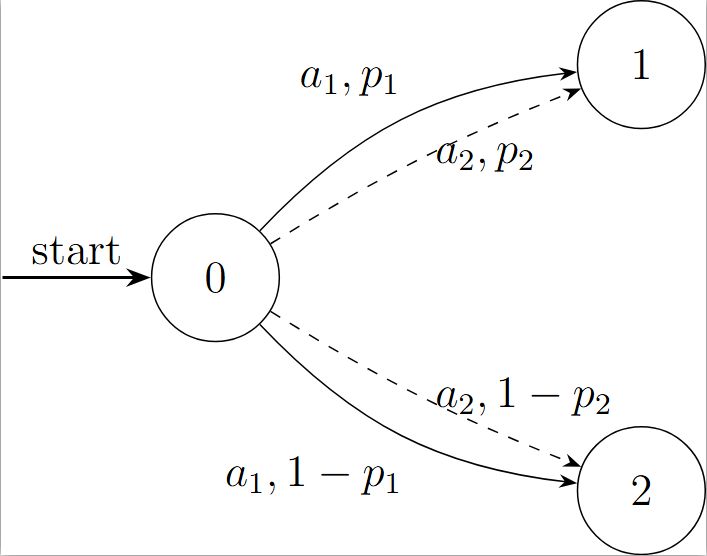
image-20250605004520337

假设我们只考虑一步决策，并且设置奖励函数为 R(⋅,⋅,1)=1R(\cdot,\cdot,1) = 1 和 R(⋅,⋅,2)=0R(\cdot,\cdot,2) = 0（只要到达状态1就给1点奖励）。假设动作的概率为 p1=0.8p_1 = 0.8 和 p2=0.6p_2 = 0.6，ρ=0.3\rho=0.3，使用L1L_1距离，则原问题可以简化为：

sup⁡d∈Δ(A) inf⁡pd⊤ps.t. ∑a∈A∣pa−p‾a∣≤∣A∣ρpa∈Δ(S)\begin{align*} \sup_{\mathbf{d}\in\Delta(\mathcal{A})}~&\inf_{\mathbf{p}}\mathbf{d}^\top \mathbf{p}\\ {\rm s.t.}~ &\sum_{a\in\mathcal{A}}\left|p_a-\overline{p}_{a}\right|\leq |\mathcal{A}|\rho\\ &p_{a}\in\Delta(\mathcal{S}) \end{align*}

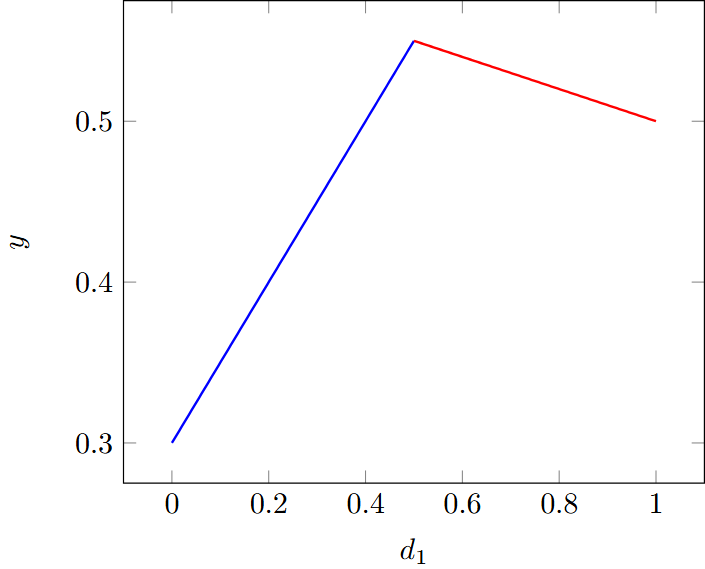
这里的目标是最优化两个概率向量 d\mathbf{d} 和 p\mathbf{p}。当 d1≥d2d_1 \geq d_2（即 d1≥0.5d_1 \geq 0.5）时，inf⁡p\inf_\mathbf{p} 将会将所有的budget（预算）用于减小 p1p_1，而当 d1<d2d_1 < d_2（即 d1<0.5d_1 < 0.5）时，inf⁡p\inf_\mathbf{p} 会将所有的 budget 用于减小 p2p_2。因此，优化结果可以表达为：

inf⁡pd⊤p={d1p1+d2(p2−0.3)=0.5d1+0.3,d1<0.5d1(p1−0.3)+d2p2=−0.1d1+0.6,d1≥0.5\inf_{\mathbf{p}}\mathbf{d}^\top\mathbf{p} = \begin{cases} d_1p_1+d_2(p_2-0.3)=0.5d_1+0.3,&d_1<0.5\\ d_1(p_1-0.3)+d_2p_2=-0.1d_1+0.6,&d_1\geq 0.5 \end{cases}

因此，当 d1=0.5d_1 = 0.5 时取得到最大值。最优的策略为 π∗=[0.5,0.5]\pi^* = [0.5, 0.5]。

image-20250605011237674

通过交换极大和极小的顺序，我们可以得到以下问题：

inf⁡p max⁡a∈A pas.t. ∑a∈A∣pa−p‾a∣≤∣A∣ρpa∈Δ(S)\begin{align*} \inf_{\mathbf{p}}~&\max_{a\in\mathcal{A}}~p_a\\ {\rm s.t.}~ &\sum_{a\in\mathcal{A}}\left|p_a-\overline{p}_{a}\right|\leq |\mathcal{A}|\rho\\ &p_{a}\in\Delta(\mathcal{S}) \end{align*}

此时，inf⁡p\inf\mathbf{p}会使p1,p2p_1,p_2同样的小，即 p1=0.55p_1 = 0.55（对应的 budget 为 0.5）和 p2=0.55p_2 = 0.55（对应的 budget 为 0.1），总的 budget 为 0.6。

如果不使得p1,p2p_1,p_2同样小，比如p1=0.5,p2=0.6p_1=0.5,p_2=0.6，则policy会选择0.6，把p1p_1降低到0.5的budget一定程度上被“浪费了”

最终得到的最优值都是0.55，但π∗\pi^*在max-min中是[0.5,0.5][0.5,0.5]，而在min-max中是[1,0][1,0]或[0,1][0,1]。

bisection 算法

Chin Pang Ho, Marek Petrik, Wolfram Wiesemann . Fast Bellman Updates for Robust MDPs. (2018)[pdf]

Recall that，交换完之后的优化问题为：

inf⁡Ps max⁡a∈AEPs,a[R(s,a,S)+γv(S)]s.t. ∑a∈ADf(Ps,a∥P‾s,a)≤∣A∣ρPs,a∈Δ(S)for all a∈A\begin{align*} \inf_{P_s}~&\max_{a\in\mathcal{A}}\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]\\ {\rm s.t.}~ &\sum_{a\in\mathcal{A}}D_f(P_{s,a}\|\overline{P}_{s,a})\leq |\mathcal{A}|\rho\\ &P_{s,a}\in\Delta(\mathcal{S})\quad\text{for all~} a \in \mathcal{A} \end{align*}

由于此时π\pi是一个确定性策略，π\pi只会选择EPs,a[R(s,a,S)+γv(S)]\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]中最大的一个。因此adversary 要改变PsP_{s}来均匀地降低所有动作下的收益（如前面例子中所提到的那样）。令

u=inf⁡Ps max⁡a∈AEPs,a[R(s,a,S)+γv(S)]u = \inf_{P_s}~\max_{a\in\mathcal{A}}\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]

此时Ps∗P_s^*满足EPs,a[R(s,a,S)+γv(S)]\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]对于所有aa均相等。令ξ\xi表示budget大小，定义

qa(ξ)= inf⁡Ps,a∈Δ(S) EPs,a[R(s,a,S)+γv(S)]s.t. Df(Ps,a∥P‾s,a)≤ξa\begin{align*} q_a(\xi) =~\inf_{P_{s,a}\in\Delta(\mathcal{S})}&~\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]\\ {\rm s.t.}&~D_f(P_{s,a}\|\overline{P}_{s,a})\leq \xi_a \end{align*}

随着ξ\xi增加，qa(ξ)q_a(\xi)会减小。下图是一个示例，假设我们有3个动作，adversary需要将每个qaq_a都调整到恰好等于uu（ξa=0\xi_a=0时比uu小的就不用调了），则用到的全部预算为ξ1+ξ2+ξ3\xi_1+\xi_2+\xi_3。

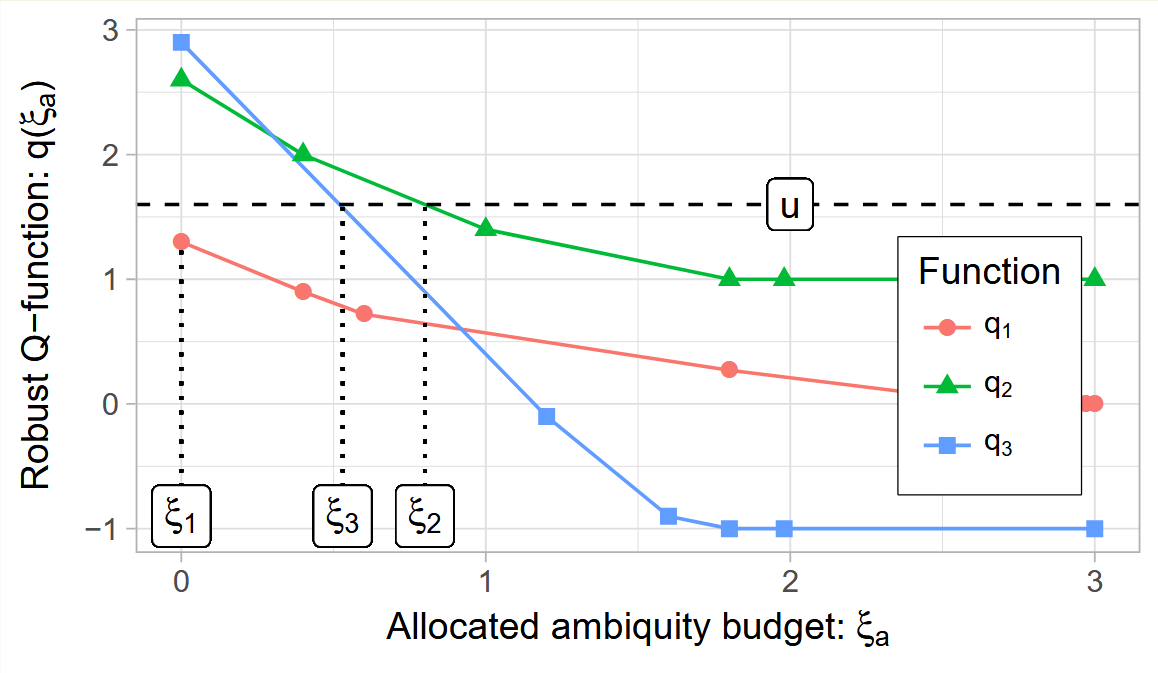
image-20250605164039955

经过以上过程，如果我们知道每个动作的ξa\xi_a，我们就可以算出qa(ξa)q_a(\xi_a)，从而算出uu。但我们需要的是从∑a∈Aqa(ξa)≤∣A∣ρ\sum_{a\in\mathcal{A}}q_a(\xi_a)\leq|\mathcal A|\rho以及最优值所有qa(ξa)q_a(\xi_a)都相等算出uu。

bisection的思路就是二分法选择uu的值，然后检测∑aξa\sum_a \xi_a是否满足约束条件。如果∑aξa>∣A∣ρ\sum_a \xi_a>|\mathcal A|\rho，则表明uu小了，反之uu大了。剩下的问题就是我们不知道给定uu，ξa\xi_a是多少，所以我们要求u=qs,a(ξa)u=q_{s,a}(\xi_a)的反函数ξa=qs,a−1(u)\xi_a = q^{-1}_{s,a}(u)：

min⁡Ps,a Df(Ps,a∥P‾s,a)s.t. EPs,a[R(s,a,S)+γv(S)]≤uPs,a∈Δ(S)for all a∈A\begin{align*} \min_{P_{s,a}}~&D_f(P_{s,a}\|\overline{P}_{s,a})\\ {\rm s.t.}~&\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v(S)\right]\leq u\\ &P_{s,a}\in\Delta(\mathcal{S})\quad \text{for all~} a \in \mathcal{A} \end{align*}

qs,a−1(u)q_{s,a}^{-1}(u)的对偶问题

Ho, Chin Pang, Marek Petrik, and Wolfram Wiesemann. Robust $\phi $-Divergence MDPs. (2022) [pdf]

由于以上问题解决起来还是比较困难，所以我们继续求上述问题的对偶问题。这里先直接给出对偶问题的形式：

max⁡λ∈R+,ν∈R −λu+ν−EP‾s,a[f∗(−λ(R(s,a,S)+γv(S))+ν)]\max_{\lambda\in\mathbb{R}_+,\nu\in\mathbb{R}}~-\lambda u+\nu -\mathbb{E}_{\overline{P}_{s,a}}\left[f^*\left(-\lambda\left(R(s,a,S)+\gamma v(S)\right)+\nu\right)\right]

KL

令ws,a(S)=R(s,a,S)+γv(S)w_{s,a}(S)=R(s,a,S)+\gamma v(S)，ws,a,min⁡=min⁡Ps,a≥0ws,aw_{s,a,\min}=\min_{P_{s,a}\geq 0}w_{s,a}，由于求解过程中，λ\lambda可能趋于0所以会出现指数爆炸的数值问题，因此需要用数值稳定版本进行求解。

对于KLKL散度，对偶问题为：

max⁡λ∈R+f(λ)=max⁡λ∈R+−λu−log⁡EP‾s,a[e−λws,a].\max_{\lambda\in\mathbb{R}_+}f(\lambda) = \max_{\lambda\in\mathbb{R}_+} - \lambda u-\log\mathbb E_{\overline{P}_{s,a}}\left[e^{-\lambda w_{s,a}}\right].

robust version

max⁡λ∈R+−λu−log⁡EP‾s,ae−λ(ws,a−ws,a,min⁡)+λws,a,min⁡\max_{\lambda\in\mathbb{R}_+} - \lambda u-\log \mathbb E_{\overline P_{s,a}}e^{-\lambda (w_{s,a}-w_{s,a,\min})} +\lambda w_{s,a,\min}

梯度为：

∂f∂λ=−u+EP‾s,a[ws,a⋅e−λws,a]EP‾s,a[e−λws,a]\frac{\partial f}{\partial \lambda} = -u+\frac{\mathbb{E}_{\overline{P}_{s,a}}\left[ w_{s,a}\cdot e^{-\lambda w_{s,a}}\right]}{\mathbb{E}_{\overline{P}_{s,a}}\left[e^{-\lambda w_{s,a}}\right]}

robust version

∂f∂λ=−u+EP‾s,a[ws,a⋅e−λ(ws,a−ws,a,min⁡)]EP‾s,a[e−λ(ws,a−ws,a,min⁡)]\frac{\partial f}{\partial \lambda} = -u+\frac{\mathbb E_{\overline P_{s,a}}\left[w_{s,a}\cdot e^{-\lambda (w_{s,a}-w_{s,a,\min})}\right]}{\mathbb E_{\overline P_{s,a}}\left[e^{-\lambda (w_{s,a}-w_{s,a,\min})}\right]}

注意到

λ∈[0,log⁡(1min⁡P‾s,a)⋅1u−min⁡w]\lambda \in \left[0,\log \left(\frac{1}{\min \overline{P}_{s,a}}\right)\cdot \frac{1}{u-\min w}\right]

又由于ff是个凹函数，因此可以用二分法来寻找最大值，如果梯度大于0，则表明λ∗\lambda^*在右侧，反正则在左侧。

proof

λmax⁡=log⁡(1min⁡P‾s,a)⋅1u−min⁡w⟺P‾s,a,min⁡⋅exp⁡(λmax⁡(u−wmin⁡))=1⟹∑s′∈SP‾s,a(s′)⋅exp⁡(λmax⁡(u−w(s′)))≥1⟺∑s′∈SP‾s,a(s′)⋅exp⁡(−λmax⁡w(s′))≥exp⁡(−λmax⁡u)⟺log⁡(∑s′∈SP‾s,a(s′)⋅exp⁡(−λmax⁡w(s′)))≥−λmax⁡u⟺f(λmax⁡)≤0\begin{align*} &\lambda_{\max} =\log \left(\frac{1}{\min \overline{P}_{s,a}}\right)\cdot \frac{1}{u-\min w}\\ &\Longleftrightarrow \overline{P}_{s,a,\min} \cdot \exp\left(\lambda_{\max}(u-w_{\min})\right) = 1\\ &\Longrightarrow \sum_{s^\prime\in\mathcal{S}}\overline{P}_{s,a}(s^{\prime})\cdot\exp\left(\lambda_{\max}(u-w(s^\prime))\right)\geq 1\\ &\Longleftrightarrow \sum_{s^\prime\in\mathcal{S}}\overline{P}_{s,a}(s^{\prime})\cdot\exp\left(-\lambda_{\max} w(s^\prime)\right)\geq \exp(-\lambda_{\max} u)\\ &\Longleftrightarrow \log\left( \sum_{s^\prime\in\mathcal{S}}\overline{P}_{s,a}(s^{\prime})\cdot\exp\left(-\lambda_{\max} w(s^\prime)\right) \right)\geq -\lambda_{\max} u\\ &\Longleftrightarrow f(\lambda_{\max})\leq 0 \end{align*}

由于ff是个凹函数，ff先增后减且f(0)=0f(0)=0，所以f(λmax⁡)≤0f(\lambda_{\max})\leq 0表明λmax⁡>λ∗\lambda_{\max}>\lambda^*。

policy

在求解出v∗v^*之后，还要反过来求解policy。我们通过对偶问题来求解policy。由于投影到R+\mathbb{R}_{+}和Δ(⋅)\Delta(\cdot)都比较方便，所以可以使用投影梯度法。分别计算对λ\lambda和da≡π(a∣s)d_a\equiv\pi(a|s)的梯度。

sup⁡π∈Δ(A),λ≥0(−λ∣A∣ρ−∑a∈Aλlog⁡EP‾s,a[exp⁡(−π(a∣s)(R(s,a,S)+γv(S))λ)])\sup_{\pi\in\Delta(\mathcal{A}),\lambda\geq 0}\left(-\lambda|\mathcal{A}|\rho-\sum_{a\in\mathcal{A}}\lambda\log\mathbb{E}_{\overline{P}_{s,a}}\left[\exp\left(-\frac{\pi(a|s)(R(s,a,S)+\gamma v(S))}{\lambda}\right)\right]\right)

∂f∂λ=−∣A∣ρ−∑a∈A[log⁡EPs,a[e−daws,a/λ]+1λEPs,a[daws,ae−daws,a/λ]EPs,a[e−daws,a/λ]].\frac{\partial f}{\partial \lambda} = - |\mathcal{A}| \rho - \sum_{a \in \mathcal{A}} \left[ \log \mathbb{E}_{P_{s,a}} \left[ e^{-d_aw_{s,a}/\lambda} \right] + \frac{1}{\lambda} \frac{\mathbb{E}_{P_{s,a}} \left[d_aw_{s,a} e^{-d_aw_{s,a}/\lambda} \right]}{\mathbb{E}_{P_{s,a}} \left[ e^{-d_aw_{s,a}/\lambda} \right]} \right].

robust version

∂f∂λ=−∣A∣ρ−∑a∈A[log⁡EPs,a[e−da(ws,a−ws,a,min⁡)/λ]−daws,a,min⁡λ+1λEPs,a[daws,ae−da(ws,a−ws,a,min⁡)/λ]EPs,a[e−da(ws,a−ws,a,min⁡)/λ]].=−∣A∣ρ−∑a∈A[log⁡EPs,a[e−da(ws,a−ws,a,min⁡)/λ]+1λEPs,a[da(ws,a−ws,a,min⁡)⋅e−da(ws,a−ws,a,min⁡)/λ]EPs,a[e−da(ws,a−ws,a,min⁡)/λ]].\begin{align*} \frac{\partial f}{\partial \lambda} &= - |\mathcal{A}| \rho - \sum_{a \in \mathcal{A}} \left[ \log \mathbb{E}_{P_{s,a}} \left[ e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda}\right]-\frac{d_aw_{s,a,\min}}{\lambda} + \frac{1}{\lambda} \frac{\mathbb{E}_{P_{s,a}} \left[d_aw_{s,a} e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda} \right]}{\mathbb{E}_{P_{s,a}} \left[ e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda} \right]} \right].\\ &=- |\mathcal{A}| \rho - \sum_{a \in \mathcal{A}} \left[ \log \mathbb{E}_{P_{s,a}} \left[ e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda}\right]+ \frac{1}{\lambda} \frac{\mathbb{E}_{P_{s,a}} \left[d_a(w_{s,a}-w_{s,a,\min})\cdot e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda} \right]}{\mathbb{E}_{P_{s,a}} \left[ e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda} \right]} \right]. \end{align*}

∂f∂da=EP‾s,a[ws,ae−daws,a/λ]EP‾s,a[e−daws,a/λ]\frac{\partial f}{\partial d_a} = \frac{\mathbb E_{\overline P_{s,a}}\left[w_{s,a}e^{-d_aw_{s,a}/\lambda}\right]}{\mathbb E_{\overline P_{s,a}}\left[e^{-d_aw_{s,a}/\lambda}\right]}

robust version

∂f∂da=EP‾s,a[ws,ae−da(ws,a−ws,a,min⁡)/λ]EP‾s,a[e−da(ws,a−ws,a,min⁡)/λ]\frac{\partial f}{\partial d_a} = \frac{\mathbb E_{\overline P_{s,a}}\left[w_{s,a}e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda}\right]}{\mathbb E_{\overline P_{s,a}}\left[e^{-d_a(w_{s,a}-w_{s,a,\min})/\lambda}\right]}

投影到单纯形上：

Projection onto the simplex code

Yunmei Chen and Xiaojing Ye, Projection Onto A Simplex

其它：sa-rec求解方法

Qt+1(s,a)=inf⁡Df(Ps,a∥P‾s,a)≤ρ EPs,a[R(s,a,S)+γvt(S)].Q_{t+1}(s,a)=\inf_{D_f(P_{s,a}\|\overline{P}_{s,a})\leq\rho}~\mathbb{E}_{P_{s,a}}\left[R(s,a,S)+\gamma v_t(S)\right].

对偶问题

sup⁡λ⩾0−λlog⁡EP‾s,a[exp⁡(−R(s,a,S)+γv(S)λ)]−λρ.\sup_{\lambda\geqslant0}-\lambda\log\mathbb E_{\overline{P}_{s,a}}\left[\exp\left(-\frac{R(s,a,S)+\gamma v(S)}{\lambda}\right)\right]-\lambda\rho.

同样地，令ws,a(S)=R(s,a,S)+γv(S)w_{s,a}(S)=R(s,a,S)+\gamma v(S)，ws,a,min⁡=min⁡Ps,a≥0ws,aw_{s,a,\min}=\min_{P_{s,a}\geq 0}w_{s,a}，

robust version

sup⁡λ⩾0−λlog⁡EP‾s,a[e−(ws,a−ws,a,min⁡)/λ]+ws,a,min⁡−λρ.\sup_{\lambda\geqslant0}-\lambda\log\mathbb E_{\overline{P}_{s,a}}\left[e^{-(w_{s,a}-w_{s,a,\min})/\lambda}\right]+w_{s,a,\min}-\lambda\rho.

求导

∂f∂λ=−ρ−[log⁡EP‾s,a[e−ws,a/λ]+1λEP‾s,a[ws,ae−ws,a/λ]EP‾s,a[e−ws,a/λ]]\frac{\partial \mathcal f}{\partial \lambda} = -\rho -\left[ \log \mathbb{E}_{\overline{P}_{s,a}} \left[ e^{-w_{s,a}/\lambda} \right] + \frac{1}{\lambda} \frac{\mathbb{E}_{\overline{P}_{s,a}} \left[w_{s,a} e^{-w_{s,a}/\lambda} \right]}{\mathbb{E}_{\overline{P}_{s,a}} \left[ e^{-w_{s,a}/\lambda} \right]} \right]

robust version

∂L∂λ=−ρ−[log⁡EP‾s,ae−(ws,a−ws,a,min⁡)/λ−ws,a,min⁡λ]−1λEP‾s,a[ws,ae−(ws,a−ws,a,min⁡)/λ]EP‾s,a[e−(ws,a−ws,a,min⁡)/λ]\begin{align*} \frac{\partial \mathcal L}{\partial \lambda} &= -\rho -\left[ \log \mathbb{E}_{\overline{P}_{s,a}} e^{-(w_{s,a}-w_{s,a,\min})/\lambda}-\frac{w_{s,a,\min}}{\lambda} \right]\\ &- \frac{1}{\lambda} \frac{\mathbb{E}_{\overline{P}_{s,a}} \left[w_{s,a} e^{-(w_{s,a}-w_{s,a,\min})/\lambda} \right]}{\mathbb{E}_{\overline{P}_{s,a}} \left[ e^{-(w_{s,a}-w_{s,a,\min})/\lambda} \right]} \end{align*}

当λ→0\lambda \rightarrow 0

f(λ)=min⁡P‾s,a(s′)>0Rs,a(s′)+γv(s′)f(\lambda)=\min_{\overline P_{s,a}(s^\prime)>0} R_{s,a}(s^\prime) + \gamma v(s^\prime)

dfdλ=−ρ−[log⁡Ps,a(smin⁡)−min⁡ws,aλ+min⁡ws,aλ]=−ρ−log⁡Ps,a(smin⁡)\frac{df}{d\lambda}=-\rho -\left[\log P_{s,a}(s_{\min})-\frac{\min w_{s,a}}{\lambda}+\frac{\min w_{s,a}}{\lambda}\right]=-\rho - \log P_{s,a}(s_{\min})

由于

λ∗∈[0,1ρ(1−γ)]\lambda^*\in[0,\frac{1}{\rho(1-\gamma)}]

因此类似地，可以使用二分法求解