Stream Algorithm

Data Warehouse

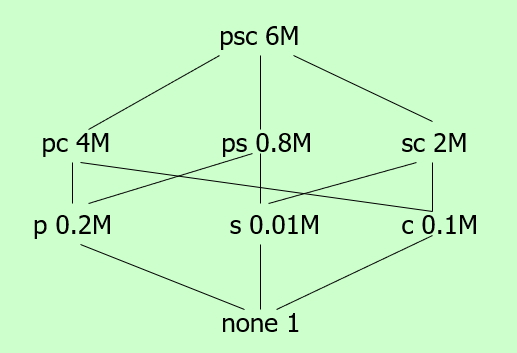
考虑这样一系列视图（view），我们希望存储其中的若干个使得总cost相比于只存储top节点节约的最多。可以使用贪婪算法来处理。

具体而言，每一轮迭代中，对于每个节点，计算储存当前节点所带来的增益，选取增益最大的并进行存储。

$\varepsilon$-deficient synopsis

1. No False Negatives

2. The difference between the estimated frequency and the true frequency is at most $\varepsilon N$.

   $$f-\tilde f\leq \varepsilon N$$

3. All items whose true frequencies less than $(s-\varepsilon)N$ are classified as infrequent items in the algorithm output

   $$\tilde f\leq(s-\varepsilon)N \rightarrow {\rm negative}$$

Sticky Algorithm

以上伪代码为了处理掷骰子部分有点复杂，人话版本：

1. 对于每个到来的数据，如果不在内存中，以1/r的概率加入。如果在内存中，count+1
2. 每当r变化的时候，对所有内存中的元素做一次删除。具体删除方式为：掷骰子，如果是反面则count -1，如果是正面则停止，如果中途count = 0则删除。
3. 最后输出满足$f+\varepsilon N\geq sN$的元素

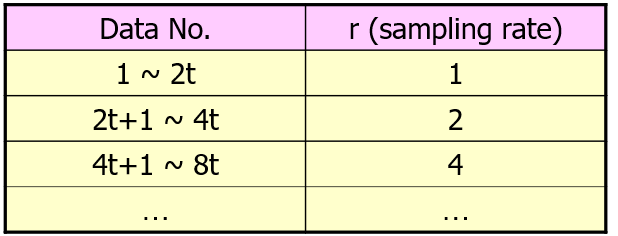
$r$的确定方式：其中$t=1/\varepsilon \cdot \log(s^{-1}\delta^{-1})$

Example

Lossy Counting Algorithm

Space Saving Algorithm

Example

Hoeffding Tree Algorithm

样本	天气	温度	是否打球
1	晴	热	否
2	晴	温暖	否
3	阴	温暖	是
4	雨	冷	是
5	雨	冷	是
6	雨	温暖	否
7	阴	冷	是

储存：$({\rm feature},{\rm attr},{\rm label})$

比如上述数据集，就要储存样本1：$({\rm feature}=\text{天气},{\rm attr}=\text{晴},{\rm label}=\text{否})$，样本3：$({\rm feature}=\text{天气},{\rm attr}=\text{阴},{\rm label}=\text{是})$等等。然后根据储存的这些数据计算information gain。

例如先读取了前4个数据，则存储应该为

$$\begin{gather*} n({\rm feature}=\text{天气},{\rm attr}=\text{晴},{\rm label}=\text{是})=0\\ n({\rm feature}=\text{天气},{\rm attr}=\text{晴},{\rm label}=\text{否})=2\\ n({\rm feature}=\text{天气},{\rm attr}=\text{阴},{\rm label}=\text{是})=1\\ n({\rm feature}=\text{天气},{\rm attr}=\text{阴},{\rm label}=\text{否})=0\\ n({\rm feature}=\text{天气},{\rm attr}=\text{雨},{\rm label}=\text{是})=1\\ n({\rm feature}=\text{天气},{\rm attr}=\text{雨},{\rm label}=\text{否})=0\\ \hline n({\rm feature}=\text{温度},{\rm attr}=\text{热},{\rm label}=\text{是})=0\\ n({\rm feature}=\text{温度},{\rm attr}=\text{热},{\rm label}=\text{否})=1\\ n({\rm feature}=\text{温度},{\rm attr}=\text{冷},{\rm label}=\text{是})=1\\ n({\rm feature}=\text{温度},{\rm attr}=\text{冷},{\rm label}=\text{否})=1\\ n({\rm feature}=\text{温度},{\rm attr}=\text{温暖},{\rm label}=\text{是})=1\\ n({\rm feature}=\text{温度},{\rm attr}=\text{温暖},{\rm label}=\text{否})=0\\ \end{gather*}$$

计算信息增益（假设使用gini index）：

$$\begin{gather*} G(D) = 1-\frac 14-\frac 14 = 0.5\\ G(\text{天气})=\frac{1}{2}\cdot 0+\frac{1}{4}\cdot 0+\frac{1}{4}\cdot 0=0\\ G(\text{温度}) = \frac{1}{4}\cdot 0+\frac{1}{2}\cdot 0.5+\frac{1}{4}\cdot 0=0.25 \end{gather*}$$

以上这些信息增益都可以通过$n$算出，而无需依赖原表

随后计算Hoeffding Bound。在本例子中$R=\log_22=1$，因此

$$\epsilon = \sqrt{\frac{\ln(1/0.05)}{2 \times 4}} \approx \sqrt{\frac{2.9957}{8}} \approx 0.61$$

我们发现

$$Gain(\text{天气})-Gain(\text{温度})=0.25<0.61$$

所以暂时不分裂，以此类推。