图片来自于：《最优化：建模、算法与理论》https://bicmr.pku.edu.cn/~wenzw/optbook.html
由于《最优化：建模、算法与理论》已经很全面，因此只是将其整理一下方便查阅。

凸函数

凸函数定义

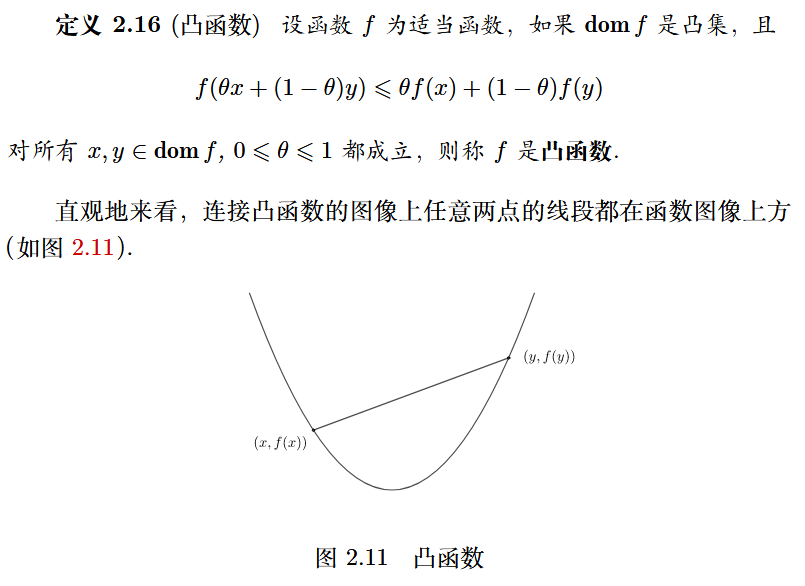
image-20250327160356654

一阶条件

image-20250327155655363 image-20250327160550217 image-20250327160616127

二阶条件

image-20250327160754646 image-20250327161637920

注：多元函数的泰勒展开和一元的有一些区别：

image-20250327162313345

由于∇2f(x)⪰0\nabla^2f(x)\succeq 0对于所有x∈domfx\in \textbf{dom} f均成立，tx+(1−t)y∈domftx+(1-t)y\in\textbf{dom} f，因此后面一坨大于等于0。

最优性条件

考虑

min⁡x∈Rnf(s)(OPT)\min_{x\in\mathbb R^n} \quad f(s)\tag{OPT}

零阶最优条件

x∗=argmin⁡x∈Rnf(x)⟺f(x∗)≤f(x)∀x∈Rnx^*=\operatorname*{argmin}_{x\in\mathbb R^n}f(x) \Longleftrightarrow f(x^*)\leq f(x) \quad \forall x\in\mathbb{R}^n

一阶必要条件

x∗=argmin⁡x∈Rnf(x)⟹∇f(x∗)=0x^*=\operatorname*{argmin}_{x\in\mathbb R^n}f(x) \Longrightarrow \nabla f(x^*)=0

image-20250327155229245

二阶必要条件

注：对于全局极小点，必要条件成立，充分条件不成立

image-20250327172217800

必要性证明

image-20250327172641028

二阶泰勒展开

f(x+d)=f(x)+∇f(x)Td+12dT∇2f(x)d+o(∥d∥2).f(x+d)=f(x)+\nabla f(x)^\mathrm{T}d+\frac{1}{2}d^\mathrm{T}\nabla^2f(x)d+o(\|d\|^2).

f(x∗+d)=f(x∗)+12dT∇2f(x)d+o(∥d∥2).f(x^*+d)=f(x^*)+\frac{1}{2}d^\mathrm{T}\nabla^2f(x)d+o(\|d\|^2).

这里好像直接用∇2f(x)⪰0\nabla^2 f(x)\succeq 0也可以直接得出零阶条件

一阶最优条件

暂时只考虑ff可微的情况，不可微的证明要用到次梯度的相关性质

当ff是凸函数的时候，

x∗=argmin⁡x∈Rnf(x)⟹∇f(x∗)=0x^*=\operatorname*{argmin}_{x\in\mathbb R^n}f(x) \Longrightarrow \nabla f(x^*)=0

证明

由于ff是凸函数，根据一阶必要条件，

f(y)≥f(x)+∇f(x)(y−x)f(y)\geq f(x)+\nabla f(x)(y-x)

因此，

f(x)≥f(x∗)+∇f(x∗)(x−x∗)=f(x∗)f(x)\geq f(x^*)+\nabla f(x^*)(x-x^*)=f(x^*)

根据零阶最优条件，得证。