Gradient Descent

方法1

对于光滑函数f(x)f(x)，在xkx^k处，希望找到一个方向dkd^k使得函数下降最快。因此考虑

ϕ(α)=f(xk+αdk)\phi(\alpha)=f(x^k+\alpha d^k)

在xkx^k处进行一阶泰勒展开，得：

ϕ(α)=f(xk)+α(∇f(xk))⊤dk+O(α2∥dk∥2)\phi(\alpha) = f(x^k)+\alpha \left(\nabla f(x^k)\right)^\top d^k + \mathcal O(\alpha^2\|d^k\|^2)

根据柯西不等式，当α\alpha足够小时，取dk=−∇f(xk)d^k=-\nabla f(x^k)会使得函数下降最快。

(∇f(xk))⊤⋅dk≥−∥∇f(xk)∥⋅∥dk∥\left(\nabla f(x^k)\right)^\top \cdot d^k \geq -\|\nabla f(x^k)\| \cdot \|d^k\|，当dk=−∇f(xk)d^k=-\nabla f(x^k)时取等。

限制α\alpha足够小时为了让O(α2∥dk∥2)\mathcal{O}(\alpha^2\|d^k\|^2)足够小，否则解就不一定是dk=−∇f(xk)d^k=-\nabla f(x^k)了。

方法2

对于光滑函数f(x)f(x)，在xkx^k处，希望在xkx^k的一个邻域求解f(xk)f(x^k)的一阶近似的最小值。具体而言，我们要求解如下问题：

xk+1=argmin⁡x f(xk)+(∇f(xk))⊤(x−xk)s.t.∥x−xk∥≤α∥∇f(xk)∥\begin{align*} x^{k+1}= \operatorname*{argmin}_{x} &~f(x^k)+\left(\nabla f(x^k)\right)^\top(x-x^k)\\ {\rm s.t.}& \|x-x^k\|\leq \alpha \|\nabla f(x^k)\| \end{align*}

约束条件只是假设，假设这个邻域的大小是由α∥∇f(xk)∥\alpha \|\nabla f(x^k)\|控制的。

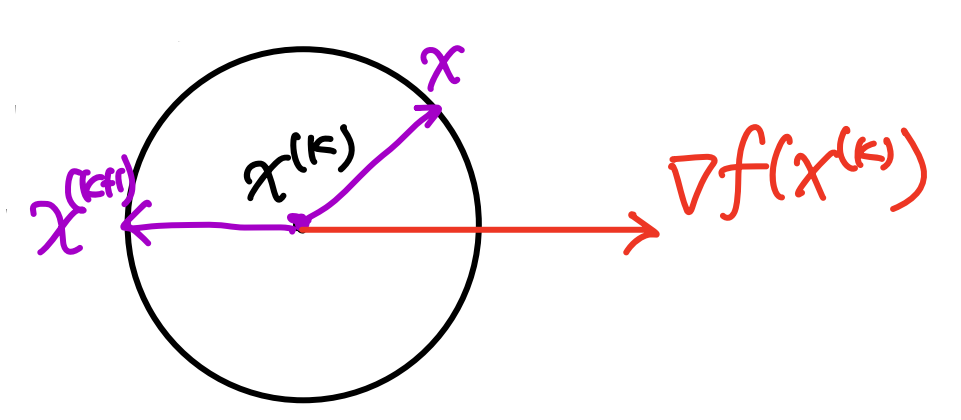
image-20250327182850704

(∇f(xk))⊤(x−xk)=cos⁡(∇f(xk),x−xk)∥∇f(xk)∥∥x−xk∥≥−∥∇f(xk)∥∥x−xk∥≥−α∥∇f(xk)∥2\begin{align*} \left(\nabla f(x^k)\right)^\top(x-x^k) &= \cos\left(\nabla f(x^k),x-x^k\right)\left\|\nabla f(x^k)\right\|\|x-x^k\|\\ &\geq-\left\|\nabla f(x^k)\right\|\|x-x^k\|\\ &\geq-\alpha\left\|\nabla f(x^k)\right\|^2 \end{align*}

只要选x−xk=−α∇f(xk)x-x^k = -\alpha\nabla f(x^k)即可满足两个等号。

因此

xk+1=xk−α∇f(xk)x^{k+1} = x^k - \alpha \nabla f(x^k)

步长选择

固定步长

假设ff是LL-利普西茨连续的，即

∥∇f(x)−∇f(y)∥≤L∥x−y∥\|\nabla f(x)-\nabla f(y)\|\leq L\|x-y\|

可以证明

∥∇2f(x)∥≤L\|\nabla^2 f(x)\|\leq L

根据二阶泰勒展开，有

f(xk+1)=f(xk)+⟨∇f(xk),xk+1−xk⟩+12⟨xk+1−xk,∇2f(xk)(xk+1−xk)⟩≤f(xk)+⟨∇f(xk),xk+1−xk⟩+L2∥xk+1−xk∥2=f(xk)−α∥∇f(xk)∥2+α2L2∥∇f(xk)∥2\begin{align*} f(x^{k+1})&=f(x^k)+\left\langle\nabla f(x^k),x^{k+1}-x^k\right\rangle+\frac 12\left\langle x^{k+1}-x^k,\nabla^2f(x^k)(x^{k+1}-x^k)\right\rangle\\ &\leq f(x^k)+\left\langle\nabla f(x^k),x^{k+1}-x^k\right\rangle+\frac L2\left\|x^{k+1}-x^k\right\|^2\\ &=f(x^k)-\alpha\left\|\nabla f(x^k) \right\|^2+\frac{\alpha^2 L}2\left\|\nabla f(x^k) \right\|^2 \end{align*}

由于我们希望f(xk+1)<f(xk)f(x^{k+1})<f(x^k)，求解

−α∥∇f(xk)∥2+α2L2∥∇f(xk)∥2<0-\alpha\left\|\nabla f(x^k) \right\|^2+\frac{\alpha^2 L}2\left\|\nabla f(x^k) \right\|^2< 0

得：α∈(0,2L)\alpha \in (0,\frac 2L)

精确线搜索

αk=argmin⁡α>0f(xk−α∇f(xk))\alpha_k = \operatorname*{argmin}_{\alpha>0} f(x^{k}-\alpha\nabla f(x^k))

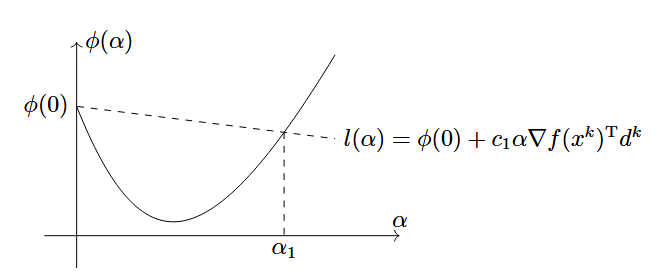
线搜索回退法（Backtracking Line Search）

在非精确线搜索算法中，选取αk\alpha_k需要满足一定的要求，这些要求被称为线搜索准则。Backtracking Line Search算法如下：

image-20250327222427808

Backtracking Line Search先选择一个初始步长，判断是否满足某个先搜索准则，如果满足，则表明我们找到的解是足够好的，可接受的，否则缩小α\alpha到γ\gamma倍。这里使用的是Armijo准则

f(xk+αdk)⩽f(xk)+c1α∇f(xk)Tdkf(x^k+\alpha d^k)\leqslant f(x^k)+c_1\alpha\nabla f(x^k)^\mathrm{T}d^k

image-20250327222725992

加速方法

Nesterov法

Nestrov算法由两步组成：第一步沿着前两步的计算方向计算一个新点， 第二步在该新点处做一步近似点梯度迭代：

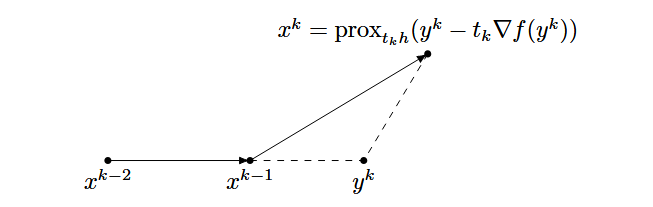
image-20250327224232898 image-20250327224438982

k−2k−1\frac{k-2}{k-1}也可以替换为其它系数，例如可以选择wk−1w_{k-1}：

λk=12(1+1+4λk−12),wk−1=λk−1−1λk\lambda_k = \frac{1}{2}\left(1 + \sqrt{1+4\lambda_{k-1}^2}\right),\quad w_{k-1}=\frac{\lambda_{k-1}-1}{\lambda_k}

Momentum法

vk+1=βkvk+∇f(xk)xk+1=xk−αvk+1\begin{align*} v^{k+1} &= \beta_k v^k + \nabla f(x^k)\\ x^{k+1}&=x^k - \alpha v^{k+1} \end{align*}

共轭梯度法

在Momentum法的基础上，选取

βk=⟨∇f(xk),∇f(xk)−∇f(xk−1)⟩⟨vk,∇f(xk)−∇f(xk−1)⟩\beta_k = \frac{\left\langle \nabla f(x^k),\nabla f(x^k)-\nabla f(x^{k-1})\right\rangle}{\left\langle v^{k},\nabla f(x^k)-\nabla f(x^{k-1})\right\rangle}

应用

最小二乘法

min⁡x∈Rn12∥Ax−b∥2\min_{x\in\mathbb R^n}\frac12\|Ax-b\|^2

GD+精确线搜索

xk+1=xk−αkA⊤(Axk−b)x^{k+1} = x^k -\alpha_kA^\top(Ax^{k}-b)

αk=argmin⁡α>0 g(α)=argmin⁡α>0 12∥A(xk−αA⊤(Axk−b))−b∥2=argmin⁡α>0 12∥Axk−b∥2−α⟨Axk−b,AA⊤(Axk−b)⟩+α22∥AA⊤(Axk−b)∥2\begin{align*} \alpha_k &=\operatorname*{argmin}_{\alpha>0} ~g(\alpha)\\ &= \operatorname*{argmin}_{\alpha>0}~ \frac12\|A(x^{k}-\alpha A^\top(Ax^{k}-b))-b\|^2\\ &= \operatorname*{argmin}_{\alpha>0}~ \frac12\|Ax^{k}-b\|^2-\alpha\langle Ax^{k}-b,AA^\top(Ax^{k}-b)\rangle+\frac{\alpha^2}2\|AA^\top(Ax^{k}-b)\|^2\\ \end{align*}

假设AA的列向量是线性无关的，由于A⊤(Axk−b)≠0A^\top (Ax^k-b)\neq 0（不是最优值），因此

g′′(α)=∥AA⊤(Axk−b)∥2>0g^{\prime\prime}(\alpha) =\|AA^\top(Ax^{k}-b)\|^2>0

根据一阶最优性条件

g′(α)=α∥AA⊤(Axk−b)∥2−⟨Axk−b,AA⊤(Axk−b)⟩=0⇔α=⟨Axk−b,AA⊤(Axk−b)⟩∥AA⊤(Axk−b)∥2=∥A⊤(Axk−b)∥2∥AA⊤(Axk−b)∥2\begin{gather*} g^\prime(\alpha) = \alpha\|AA^\top(Ax^{k}-b)\|^2-\langle Ax^{k}-b,AA^\top(Ax^{k}-b)\rangle=0\\ \Leftrightarrow \alpha = \frac{\langle Ax^{k}-b,AA^\top(Ax^{k}-b)\rangle}{\|AA^\top(Ax^{k}-b)\|^2} =\frac{\|A^\top(Ax^{k}-b)\|^2}{\|AA^\top(Ax^{k}-b)\|^2} \end{gather*}

Steepest Descent Algorithm

for k=0,1,2,⋯gk=A⊤(Axk−b)αk=∥gk∥2∥Agk∥2xk+1=xk−αkgkend\begin{align*} &\text{for}~ k=0,1,2,\cdots\\ &\quad\quad g^k = A^\top (Ax^k-b)\\ &\quad\quad \alpha_k = \frac{\|g^k\|^2}{\|Ag^k\|^2}\\ &\quad\quad x^{k+1} = x^k-\alpha_kg^k\\ &\text{end} \end{align*}

每个循环需要计算2次AA的矩阵-向量乘法和1次A⊤A^\top的矩阵-向量乘法，但是可以减少到1次AA的矩阵-向量乘法和1次A⊤A^\top的矩阵-向量乘法。具体而言，要储存gk−1g^{k-1}和Agk−1Ag^{k-1}

for k=1,2,3⋯gk=gk−1−αkA⊤(Agk−1)一次A⊤矩阵-向量乘法αk=∥gk∥2∥Agk∥2 一次A矩阵-向量乘法xk+1=xk−αkgkend\begin{align*} &\text{for}~ k=1,2,3\cdots\\ &\quad\quad g^k = g^{k-1}-\alpha_kA^\top(Ag^{k-1})\quad \text{一次}A^\top\text{矩阵-向量乘法}\\ &\quad\quad \alpha_k = \frac{\|g^k\|^2}{\|Ag^k\|^2}\quad\quad\quad\quad\quad\quad~ \text{一次}A\text{矩阵-向量乘法}\\ &\quad\quad x^{k+1} = x^k-\alpha_kg^k\\ &\text{end} \end{align*}

将Agk−1Ag^{k-1}写作uk−1u_{k-1}

g0=A⊤(Ax0−b)u0=Ag0for k=1,2,3⋯gk=gk−1−αkA⊤uk−1一次A⊤矩阵-向量乘法uk=Agk   一次A矩阵-向量乘法αk=∥gk∥2∥uk∥2xk+1=xk−αkgkend\begin{align*} &g^0=A^\top(Ax^0-b)\\ &u^0 = A g_0\\ &\text{for}~ k=1,2,3\cdots\\ &\quad\quad g^k = g^{k-1}-\alpha_kA^\top u^{k-1}\quad \text{一次}A^\top\text{矩阵-向量乘法}\\ &\quad\quad u^k = Ag^k\quad\quad\quad\quad\quad\quad~~~ \text{一次}A\text{矩阵-向量乘法}\\ &\quad\quad \alpha_k = \frac{\|g^k\|^2}{\|u^k\|^2}\quad \\ &\quad\quad x^{k+1} = x^k-\alpha_kg^k\\ &\text{end} \end{align*}

共轭梯度法

gk=A⊤(Ax−b)pk=gk+βkpk−1xk+1=xk−αkpk\begin{align*} g^k &= A^\top (Ax-b)\\ p^k &=g^k+\beta_kp^{k-1}\\ x^{k+1}&=x^{k}-\alpha_kp^k \end{align*}

需要求解αk,βk\alpha_k,\beta_k使得f(xk+1)f(x^{k+1})最小。首先由于αk\alpha_k是最优的，因此：

αk=argmin⁡αg(α)=argmin⁡α12∥A(xk−αpk)−b∥2=argmin⁡α12∥Axk−b∥2−α⟨Axk−b,Apk⟩+α22∥Apk∥2\begin{align*} \alpha_k &= \operatorname*{argmin}_{\alpha} g(\alpha)\\ &=\operatorname*{argmin}_{\alpha} \frac12\|A(x^k-\alpha p^k)-b\|^2\\ &=\operatorname*{argmin}_{\alpha} \frac12\|Ax^k-b\|^2-\alpha\langle Ax^k-b,A p^k \rangle+\frac{\alpha^2}2\|A p^k\|^2\\ \end{align*}

根据一阶最优性条件，

g′(α)=α∥Apk∥2−α⟨Axk−b,Apk⟩=0⇔α=⟨Axk−b,Apk⟩∥Apk∥2=⟨A⊤(Axk−b),pk⟩∥Apk∥2=⟨gk,pk⟩∥Apk∥2\begin{gather*} g^\prime(\alpha)=\alpha\|Ap^k\|^2-\alpha\langle Ax^k-b,A p^k \rangle=0\\ \Leftrightarrow \alpha = \frac{\langle Ax^k-b,A p^k \rangle}{\|Ap^k\|^2}=\frac{\langle A^\top (Ax^k-b),p^k \rangle}{\|Ap^k\|^2}=\frac{\langle g^k,p^k \rangle}{\|Ap^k\|^2} \end{gather*}

αk\alpha_k的这个最优形式可以得到：

⟨gk+1,pk⟩=⟨A⊤(A(xk−αkpk)−b),pk⟩=⟨A⊤A(xk−b)−αkA⊤Apk,pk⟩=⟨gk−αkA⊤Apk,pk⟩=⟨gk,pk⟩−αk⟨A⊤Apk,pk⟩=⟨gk,pk⟩−⟨gk,pk⟩∥Apk∥2⟨Apk,Apk⟩=0\begin{align*} \langle g^{k+1},p^k\rangle &= \langle A^\top (A(x^k-\alpha_k p_k)-b),p^k\rangle\\ &= \langle A^\top A(x^k-b)-\alpha_kA^\top A p_k,p^k\rangle\\ &= \langle g^k-\alpha_kA^\top A p_k,p^k\rangle\\ &=\langle g^k,p^k\rangle-\alpha_k\langle A^\top A p_k,p^k\rangle\\ &=\langle g^k,p^k\rangle-\frac{\langle g^k,p^k \rangle}{\|Ap^k\|^2}\langle A p_k,Ap^k\rangle =0 \end{align*}

接下来求解βk\beta_k

(αk,βk)=argmin⁡α,βE(α,β)=argmin⁡α,βf(xk−α(gk+βpk−1))(\alpha_k,\beta_k) = \operatorname*{argmin}_{\alpha,\beta} E(\alpha,\beta) =\operatorname*{argmin}_{\alpha,\beta}f\big(x^k-\alpha(g^k+\beta p^{k-1})\big)

denote θ=αβ\theta=\alpha \beta

E(α,θ)=12∥A(xk−αgk−θpk−1)−b∥2=12∥(b−Axk)+αAgk+θApk−1)∥2=12(∥b−Axk∥2+α2∥Agk∥2+θ2∥Apk−1∥2+2α⟨b−Axk,Agk⟩+2θ⟨b−Axk,Apk−1⟩+2αθ⟨Agk,Apk−1⟩)\begin{align*} E(\alpha,\theta)&=\frac12\Big\|A(x^k-\alpha g^k-\theta p^{k-1})-b\Big\|^2\\ &=\frac12\Big\|(b-Ax^k)+\alpha A g^k+\theta A p^{k-1})\Big\|^2\\ &=\frac12\Big(\|b-Ax^k\|^2+\alpha^2\|Ag^k\|^2+\theta^2\|Ap^{k-1}\|^2\\&+2\alpha\langle b-Ax^k,Ag^k \rangle+2\theta\langle b-Ax^k,Ap^{k-1} \rangle +2\alpha\theta\langle Ag^k,Ap^{k-1} \rangle\Big) \end{align*}

∂E∂θ=θ∥Apk−1∥2+θ⟨b−Axk,Apk−1⟩+2α⟨Agk,Apk−1⟩=θ∥Apk−1∥2+θ⟨A⊤(b−Ax)k,pk−1⟩+α⟨Agk,Apk−1⟩=θ∥Apk−1∥2+α⟨Agk,Apk−1⟩=0\begin{align*} \frac{\partial E}{\partial \theta}&=\theta\|Ap^{k-1}\|^2+\theta\langle b-Ax^k,Ap^{k-1} \rangle+2\alpha\langle Ag^k,Ap^{k-1} \rangle\\ &=\theta\|Ap^{k-1}\|^2+\theta\langle A^\top(b-Ax)^k,p^{k-1} \rangle+\alpha\langle Ag^k,Ap^{k-1} \rangle\\ &=\theta\|Ap^{k-1}\|^2+\alpha\langle Ag^k,Ap^{k-1} \rangle=0 \end{align*}

θk=−α⟨Agk,Apk−1⟩∥Apk−1∥2⇔βk=−⟨Agk,Apk−1⟩∥Apk−1∥2\theta_k=-\alpha\frac{\langle Ag^k,Ap^{k-1} \rangle}{\|Ap^{k-1}\|^2} \Leftrightarrow \beta_k=-\frac{\langle Ag^k,Ap^{k-1} \rangle}{\|Ap^{k-1}\|^2}

Conjugate Gradient for Least Squares

p−1=0for k=0,1,2,⋯gk=A⊤(Axk−b)βk=−⟨Agk,Apk−1⟩∥Apk−1∥2pk=gk+βkpk−1αk=⟨gk,pk⟩∥Apk∥2xk+1=xk−αkpkend\begin{align*} &p^{-1}=0\\ &\text{for}~ k=0,1,2,\cdots\\ &\quad\quad g^k = A^\top (Ax^k-b)\\ &\quad\quad \beta_k=-\frac{\langle Ag^k,Ap^{k-1} \rangle}{\|Ap^{k-1}\|^2}\\ &\quad\quad p^k =g^k+\beta_kp^{k-1}\\ &\quad\quad \alpha_k = \frac{\langle g^k,p^k\rangle}{\|Ap^k\|^2}\\ &\quad\quad x^{k+1} = x^k-\alpha_kp^k\\ &\text{end} \end{align*}

线性方程组

min⁡x∈Rn Ax=bs.t. A∈Rn×n is SPD\begin{align*} \min_{x\in\mathbb R^n} &~Ax=b\\ {\rm s.t.}&~A\in\mathbb R^{n\times n} ~\text{is SPD} \end{align*}

等价于

min⁡x∈Rn 12x⊤Ax−x⊤b\begin{align*} \min_{x\in\mathbb R^n} &~\frac12 x^\top Ax-x^\top b \end{align*}

Steepest Descent（GD+精确线搜索）

xk+1=xk−αk(Axk−b)x^{k+1} = x^{k} - \alpha_k(Ax^{k} - b)

其中

αk=argmin⁡α>0g(α)=argmin⁡α>0f(xk−α(Axk−b))=12(xk−α(Axk−b))⊤A(xk−α(Axk−b))−(xk−α(Axk−b))⊤b=12(xk)⊤Axk−(xk)⊤b−α(xk)⊤A(Axk−b)+α22(Axk−b)⊤A(Axk−b)+α(Axk−b)⊤b\begin{align} \alpha_{k}&=\operatorname*{argmin}_{\alpha>0}g(\alpha)\\ &=\operatorname*{argmin}_{\alpha>0}f(x^{k}-\alpha(Ax^{k}-b))\\ &=\frac12\big(x^{k}-\alpha(Ax^{k}-b)\big)^\top A\big(x^{k}-\alpha(Ax^{k}-b)\big)-\big(x^{k}-\alpha(Ax^{k}-b)\big)^\top b\\ &=\frac 12 (x^k)^\top Ax^k-(x^k)^\top b\\ &-\alpha(x^k)^\top A(Ax^{k}-b)+\frac{\alpha^2}2(Ax^k-b)^\top A(Ax^k-b)+\alpha(Ax^k-b)^\top b\\ \end{align}

g′(α)=−(xk)⊤A(Axk−b)+α(Axk−b)⊤A(Axk−b)+(Axk−b)⊤b=−((xk)⊤A−b⊤)(Axk−b)+α(Axk−b)⊤A(Axk−b)=0\begin{align*} g^\prime(\alpha)&=-(x^k)^\top A(Ax^k -b)+\alpha(Ax^k-b)^\top A(Ax^k-b)+(Ax^k-b)^\top b\\ &=-((x^k)^\top A -b^\top)(Ax^k -b) +\alpha(Ax^k-b)^\top A(Ax^k-b)=0 \end{align*}

αk=∥Axk−b∥2⟨Axk−b,A(Axk−b)⟩\alpha_k =\frac{\|Ax^k-b\|^2}{\langle Ax^k-b,A(Ax^k-b)\rangle}

Steepest Descent for Linear Equation

for k=0,1,2,⋯gk=Axk−bαk=∥gk∥2⟨gk,Agk⟩xk+1=xk−αkgkend\begin{align*} &\text{for}~ k=0,1,2,\cdots\\ &\quad\quad g^k = Ax^k-b\\ &\quad\quad \alpha_k = \frac{\|g^k\|^2}{\langle g^k,Ag^k\rangle}\\ &\quad\quad x^{k+1} = x^k-\alpha_kg^k\\ &\text{end} \end{align*}

共轭梯度法

gk=Ax−bpk=gk+βkpk−1xk+1=xk−αkpk\begin{align*} g^k &= Ax-b\\ p^k &=g^k+\beta_kp^{k-1}\\ x^{k+1}&=x^{k}-\alpha_kp^k \end{align*}

需要求解αk,βk\alpha_k,\beta_k使得f(xk+1)f(x^{k+1})最小。首先由于αk\alpha_k是最优的，类似的，我们有：

αk=arg⁡min⁡α>0f(xk−αkpk)=⟨p(k),g(k)⟩⟨pk,Agk⟩\begin{align} \alpha_{k}&=\arg\min_{\alpha>0}f(x^{k}-\alpha_{k}p^{k})\\&=\frac{\langle p^{(k)},g^{(k)}\rangle}{\langle p^{k},Ag^{k}\rangle} \end{align}

以及⟨gk,pk−1⟩=0\langle g^{k},p^{k-1}\rangle=0。

接下来求解βk\beta_k

(αk,βk)=argmin⁡α,βE(α,β)=argmin⁡α,βf(xk−α(gk+βpk−1))(\alpha_k,\beta_k) = \operatorname*{argmin}_{\alpha,\beta} E(\alpha,\beta) =\operatorname*{argmin}_{\alpha,\beta}f\big(x^k-\alpha(g^k+\beta p^{k-1})\big)

展开，带入⟨gk,pk−1⟩=0\langle g^{k},p^{k-1}\rangle=0，得：

βk=−⟨gk,Apk−1⟩⟨pk−1,Apk−1⟩\beta_k = -\frac{\langle g^{k},Ap^{k-1}\rangle}{\langle p^{k-1},Ap^{k-1}\rangle}

p−1=0for k=0,1,2,⋯gk=Axk−bβk=−⟨gk,Apk−1⟩⟨pk−1,Apk−1⟩pk=gk+βkpk−1αk=⟨p(k),g(k)⟩⟨pk,Agk⟩xk+1=xk−αkpkend\begin{align*} &p^{-1}=0\\ &\text{for}~ k=0,1,2,\cdots\\ &\quad\quad g^k = Ax^k-b\\ &\quad\quad \beta_k=-\frac{\langle g^{k},Ap^{k-1}\rangle}{\langle p^{k-1},Ap^{k-1}\rangle}\\ &\quad\quad p^k =g^k+\beta_kp^{k-1}\\ &\quad\quad \alpha_k = \frac{\langle p^{(k)},g^{(k)}\rangle}{\langle p^{k},Ag^{k}\rangle}\\ &\quad\quad x^{k+1} = x^k-\alpha_kp^k\\ &\text{end} \end{align*}