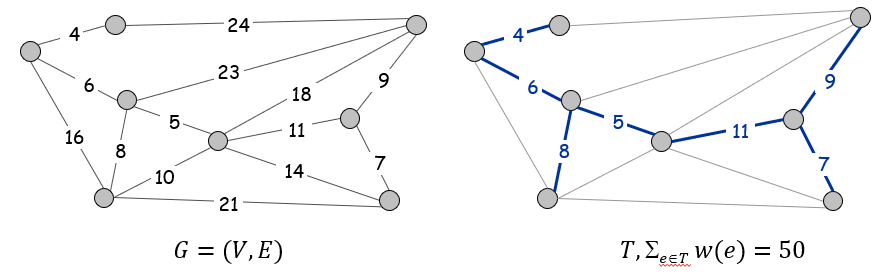
在一个 带权无向连通图 中，生成树（Spanning Tree）是包含图中所有顶点且边数最少的连通子图。而 最小生成树 是所有生成树中边的权重之和最小的那棵树。

image-20250317113101574

Prim’s Algorithm

Algorithm

思路：

  1. 初始化：
    任选一个顶点作为初始子图（即生成树的起点），此时生成树包含 0条边，仅有一个顶点。
  2. 贪心扩展：
    重复以下步骤，直到所有顶点都被包含在生成树中：
    • 寻找最小边：从当前生成树的所有顶点出发，选择一条 权重最小的边，要求这条边连接生成树内的顶点（已选集合）和生成树外的顶点（未选集合）。
    • 加入生成树：将这条边及其连接的未选顶点加入生成树，保证不形成环路。
  3. 终止条件：
    当生成树包含图中所有顶点时停止（边数 = 顶点数 - 1）。
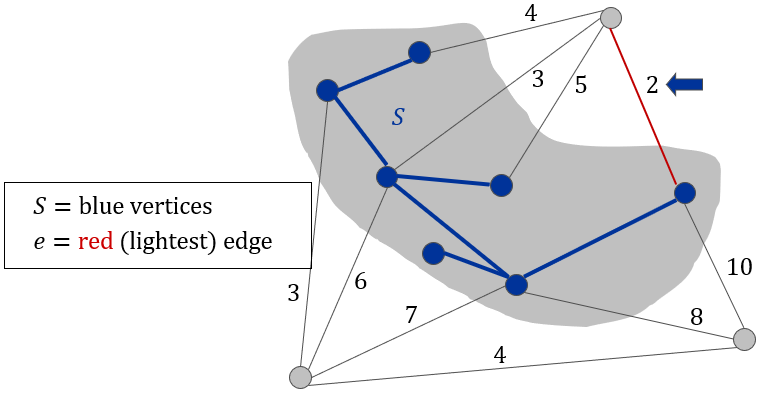
image-20250317164532256

算法：

image-20250317165301347

我们需要维护一个“所有点到树的最小距离”的优先队列。例如对于上图的三个灰色节点分别要储存2，8，3。

当新顶点 uu 被加入生成树时，遍历 uu 的所有邻接顶点 vv，如果vv不在树中，且u,vu,v的距离比最小距离要小，则更新最小距离。由于生成树每次仅扩展一个顶点 uu，只有 uu 的新邻接边可能为未选顶点 vv 提供更小的权重路径，因此著需要检查uu的节点即可。每次更新顶点 vv 的最小权重后，立即对优先队列执行 decrease-key 操作，确保堆结构始终反映最新的最小权重值。

不过由于大部分现有的语言的最小堆都不自带decrease-key，所以可以通过使用insert key来更新距离，这样同样可以保证最小的排在最前面。但是这样会导致优先队列中有多个相同节点，因此在extract-min的时候还要检查一下这个节点是否已经处理过了。

image-20250317182209446

计算复杂度O(Elog⁡V)\mathcal{O}(E\log V)

正确性

cut lemma

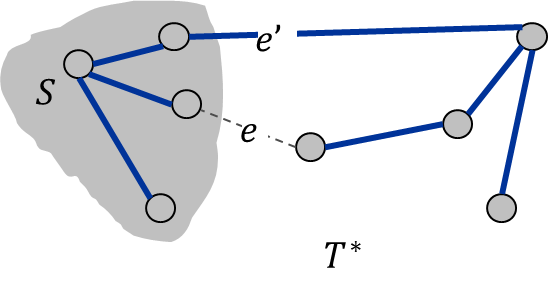
假设所有的边都是有权重且唯一的，令SS为任意节点的子集，ee是连接SS和V−SV-S的权重最小的一条边，则ee必然在属于所有的最小生成树。（如果权重不唯一，则是必然属于某个最小生成树）

proof

假设T∗T^*是某个MST，e=edge(u,v)e={\rm edge}(u,v)且e∉T∗e\notin T^*，则存在某条边e′e^\prime连接SS和V−SV-S（否则不连通），将e′e^\prime换成ee会使得权重和减小，则T∗T^*不是MST，冲突。

image-20250317220257882

Kruskal’s Algorithm

思路：对所有边按权重进行排序，从小到达依次考虑每条边。如果添加ee产生了环，则删掉ee，否则讲ee加入到TT中

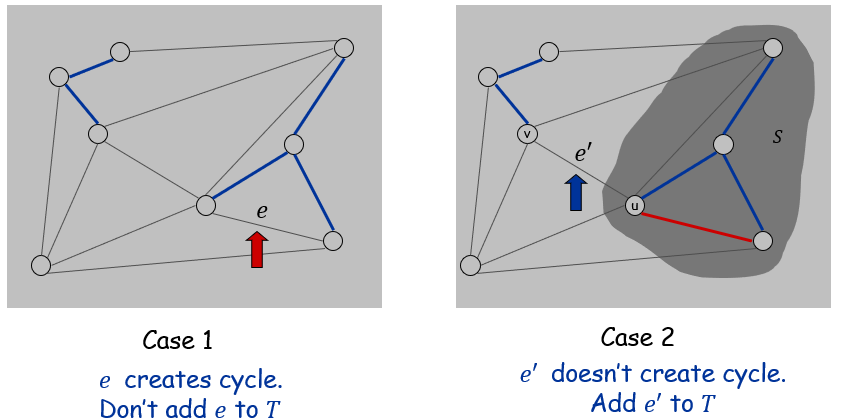
image-20250317221336526

Kruskal’s Algorithm的关键问题在于如何检测环，如果每次使用DFT的话时间复杂度为O(EV)\mathcal{O}(EV)

observations

假设所有节点可以分为T1,⋯ ,TnT_1,\cdots,T_n，不能成环就是说当添加一条新边时，只能在TiT_{i}和TjT_j（i≠ji\neq j）中添加。

因此我们需要维护这样一个数据结构（union-find）：

  • find-set(u)：给定uu，查找uu属于哪个集合
  • union(u,v)：给定两个节点u,vu,v，将u,vu,v属于的两个集合合并

可以使用以下结构：根节点是该集合的表示，当合并时，将一个树的根节点指向另一个树的根节点

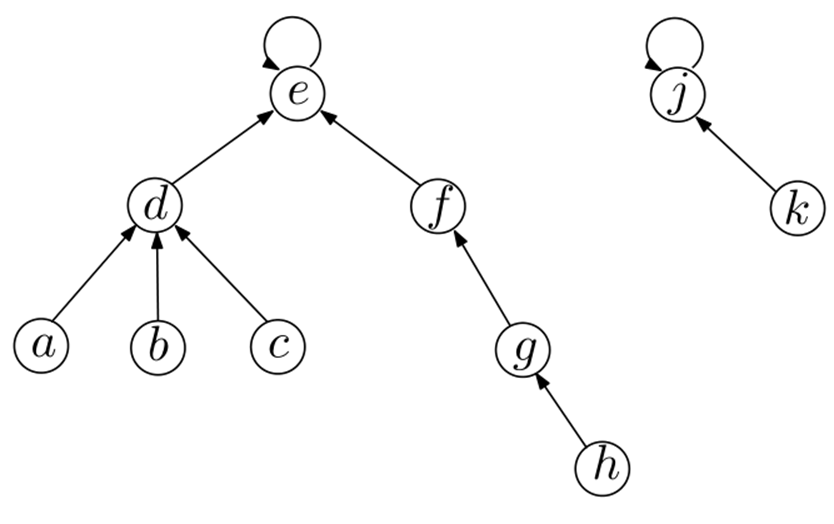
image-20250317223647508 image-20250317223859983

但是在最坏情况下执行find-set(x)可能需要O(V)\mathcal{O}(V)的时间

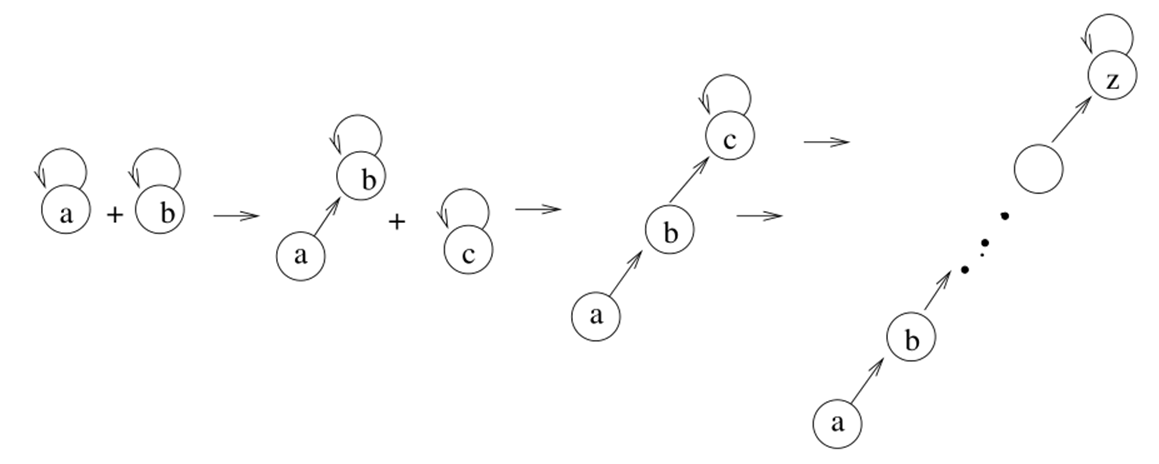
image-20250317224004248

以下是两点关于union-find的改进

  1. union by height：在合并时将height更低的集合的根节点指向height更高的根节点

    image-20250317224302643

    这里height储存在根节点中（只有根节点中的height是有效的），height增加只会发生在两个树高度相同时（注意一定是新作为根节点的节点的高度加1）

    使用union by height后，find-set的时间复杂度为O(log⁡n)\mathcal{O}(\log n)

    proof

    归纳法：假设任意高度为hh的树至少包含2h2^h个节点

    最开始时h(x)=0h(x)=0，size(x)=1{\rm size}(x)=1，1≥201\geq 2^0，满足条件

    对于两个集合x,yx,y，假设合并后的集合为zz

    • h(x)≠h(y)h(x)\neq h(y)，则h(z)=max⁡{h(x),h(y)}h(z)=\max\{h(x),h(y)\}：

      size(z)=size(x)+size(y)≥2h(x)+2h(y)≥2max⁡{h(x),h(y)}=2h(z){\rm size}(z) = {\rm size}(x)+{\rm size}(y)\geq2^{h(x)}+2^{h(y)}\geq 2^{\max\{h(x),h(y)\}}=2^{h(z)}

    • h(x)=h(y)h(x)=h(y)，则h(z)=h(x)+1h(z)=h(x)+1

      size(z)=size(x)+size(y)≥2h(x)+2h(y)=2h(x)+1=2h(z){\rm size}(z) = {\rm size}(x)+{\rm size}(y)\geq2^{h(x)}+2^{h(y)}=2^{h(x)+1}=2^{h(z)}

      由于对于任何树，一定包含≤n\leq n个节点，因此高度小于log⁡n\log n

  2. pass compression

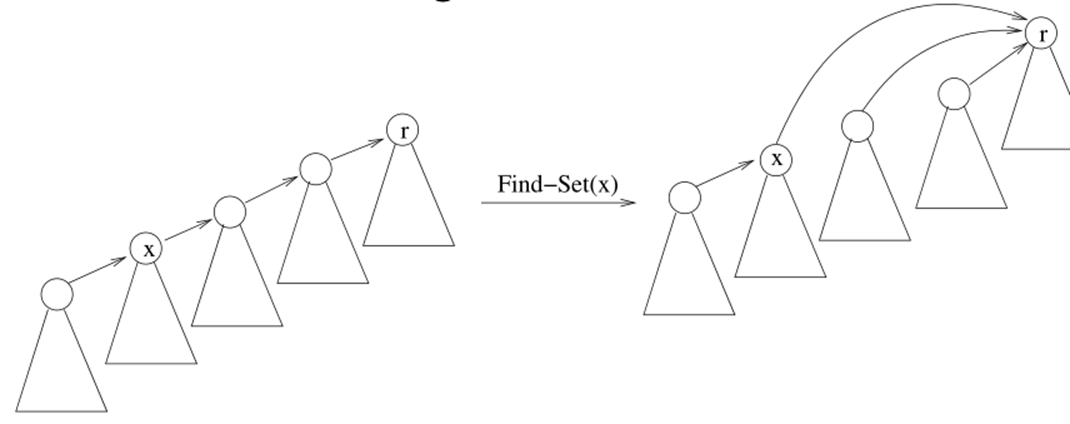
    image-20250318001656736

    在find-set(x)的时候从节点xx开始，沿着父指针向上递归查找，直到找到根节点，然后回溯，将路径上所有节点直接指向根节点

计算复杂度O(Elog⁡V)\mathcal{O}(E\log V)（使用union by height），O(E)\mathcal{O}(E)（使用union by height+pass compression）

Kruskal’s Algorithm的正确性同样由cut lemma 给出