Algorithm
思想:从点s开始,探索所有相邻节点,一层一层探索
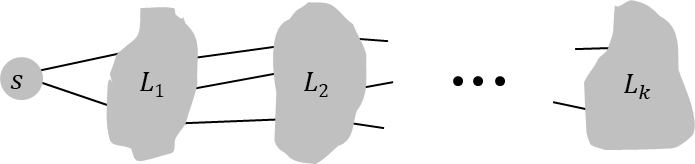
- L0={s}
- L1是s的所有邻居
- L2是L1中所有的点的邻居,但是不包括s
- ⋯
- Lk是Lk−1中所有的点的邻居,但是不包括L0,⋯,Lk−1中的点

color = white表示该点从未被访问过,color = gray 表示该点正在处理中,color = black表示改点已处理完
Example
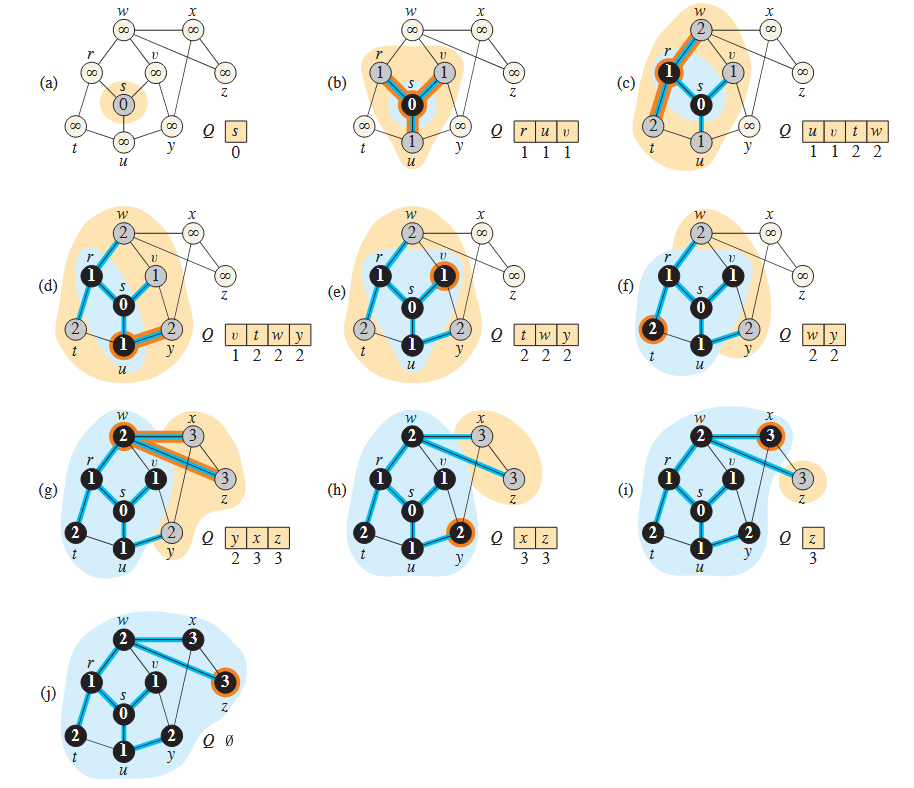
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Node:
def __init__(self, value):
self.value = value
self.color = 0
self.d = float('inf')
self.p = None
nodes = {n: Node(n) for n in ['r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']}
G = {nodes['s']: [nodes['r'], nodes['u'], nodes['v']],
nodes['r']: [nodes['t'], nodes['w']],
nodes['t']: [nodes['r'], nodes['u']],
nodes['u']: [nodes['t'], nodes['s'], nodes['y']],
nodes['y']: [nodes['u'], nodes['v'], nodes['x']],
nodes['v']: [nodes['s'], nodes['w']],
nodes['w']: [nodes['r'], nodes['v'], nodes['x'], nodes['z']],
nodes['x']: [nodes['w'], nodes['y'], nodes['z']],
nodes['z']: [nodes['w'], nodes['x']]}
def BFS(graph, start):
start.color = 1
start.d = 0
start.p = None
queue = [start]
while queue:
u = queue.pop(0)
for v in graph[u]:
if v.color == 0:
v.color = 1
v.d = u.d + 1
v.p = u
queue.append(v)
u.color = 2
BFS(G, nodes['s'])
for n in G.keys():
print(f"{n.value}:d={n.d}, p={n.p.value if n.p else None}")
|
Application
1.寻找connected components
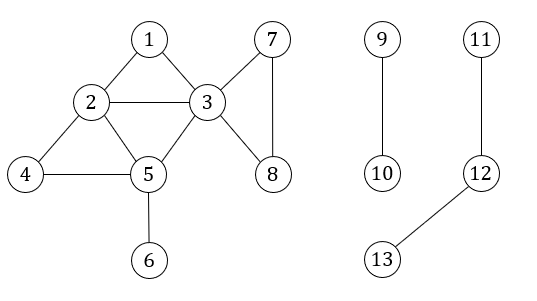
多次BFS即可
2.国际象棋中骑士到达某一点的最短移动次数

按照骑士的移动规则定义边,比如(x,y)和(x+2,y-1)之间有一条边
3.检测bipartite graph
如果可以将一个图的所有点分为两簇S,V−S,S中的点只与V−S的点相连,而不和S中的点相连,对于V−S也类似。
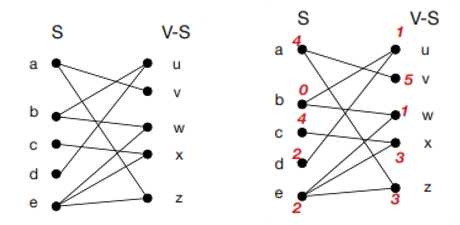
注意到如果从左侧出发,那么所有到右侧的点的距离都是奇数,所有到左侧点的距离都是偶数。
从任一点出发,进行BFS,将所有距离为偶数的点分到S,所有距离为奇数的点分到V−S。
当且仅当所有edge(u,v)两端的节点的距离的奇偶性不同的时候,G是一个bipartite graph
4.Minmum height trees
给定一个有n个节点的树,选择一个节点作为root使得树的高度最小
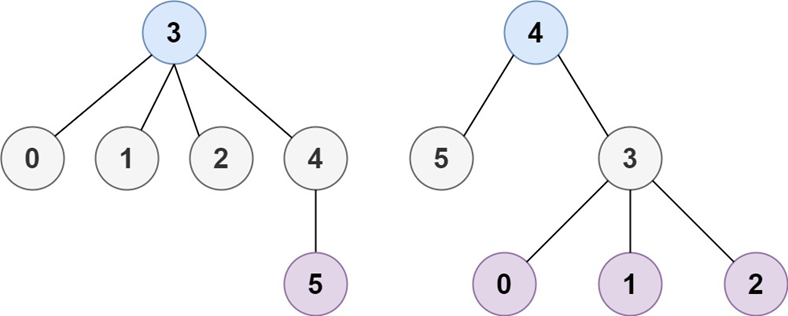
使用一个节点u连接所有叶节点,do BFS,最后一层即为要选择的根节点






