Singular Value Decomposition (SVD)

封面：Singular Value Decomposition (SVD) in Python - AskPython

eigenvalue decomposition for symmetric matrix

令 $A\in\mathbb R^{n\times n}$ 为一个对称矩阵(i.e.$A^\top = A$). 那么存在

$$A = U\Lambda U^\top$$

其中

$$\begin{gather*} U = [u_1,u_2,\cdots,u_n]\in\mathbb R^{n\times n} ~\text{is orthogonal}\\ \Lambda = \begin{bmatrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{bmatrix} \in\mathbb R^{n\times n}~\text{is a diagonal matrix} \end{gather*}$$

且$\lambda_i,i=1,\cdots,n$是$A$的特征值,$u_i,i=1,\cdots,n$是对应的特征向量

proof

1. 证明所有$A$的特征值均为实数

2. 通过归纳法证明存在$A = U\Lambda U^\top$

   如果$n=1$

   $$A = 1\cdot A\cdot 1$$

   假设对于任意$A_k\in\mathbb R^{k\times k}$ 存在一个decomposition：$A_k=U_k\Lambda_kU_k^\top$

   对于任意的$A_{k+1}\in\mathbb R^{(k+1)\times (k+1)}$，令$(\lambda,u)$是$A_{k+1}$的一个特征值-特征向量满足$A_{k+1}u=\lambda u,\|u\|_2 =1$

   因为$u\in\mathbb R^{k+1}$是单位向量，因此可以将其扩展成一个$\mathbb R^{k+1}$的正交基, denoted by $Q = [u,P]$

   $$\begin{gather*} Q^\top A_{k+1}Q = \begin{bmatrix}u^\top\\P^\top\end{bmatrix}A_{k+1} \begin{bmatrix}u&P\end{bmatrix}\\ = \begin{bmatrix}u^\top A_{k+1}u&u^\top A_{k+1}P\\ P^\top A_{k+1}u&P^\top A_{k+1}P\end{bmatrix} \end{gather*}$$

   其中，

   $$\begin{align*} u^\top A_{k+1}u&=u^\top(\lambda u)=\lambda u^\top u = \lambda\\ P^\top A_{k+1}u &= P^\top(\lambda u)=\lambda P^\top u=0\\ u^\top A_{k+1}P&=(P^\top A_{k+1}u)^\top=0^\top=0\\ (P^\top A_{k+1}P)^\top&=P^\top A_{k+1}^\top P=P^\top A_{k+1}P\Rightarrow P^\top A_{k+1}P~\text{is symmetric} \end{align*}$$

   根据归纳法的假设，存在$S,D\in\mathbb R^{n\times n }$满足

   $$P^\top A_{k+1}P=SDS^\top$$

   因此

   $$\begin{gather*} Q^\top A_{k+1}Q = \begin{bmatrix}\lambda&0\\0&SDS^\top\end{bmatrix}=\begin{bmatrix}1&\\&S\end{bmatrix}\begin{bmatrix}\lambda&\\&D\end{bmatrix}\begin{bmatrix}1&\\&S^\top\end{bmatrix}\\ A_{k+1} = Q\begin{bmatrix}1&\\&S\end{bmatrix}\begin{bmatrix}\lambda&\\&D\end{bmatrix}\begin{bmatrix}1&\\&S^\top\end{bmatrix}Q^\top\\ =U_{k+1}\Lambda_{k+1}U_{k+1}^\top \end{gather*}$$

3. 接下来证明$\Lambda$是特征值，$U$是对应的特征向量

   $$\begin{gather*} A = U\Lambda U^\top \Leftrightarrow AU = U\Lambda\\ \Rightarrow A[u_1,\cdots,u_n] = [u_1,\cdots,u_n] \Lambda =[\lambda_1 u_1,\cdots \lambda_n u_n]\\ \Leftrightarrow Au_i = \lambda_iu_i \end{gather*}$$

Singular value decomposition

令$A\in\mathbb R^{m\times n}$, 其中 $m\geq n$，则$A^\top A$ 是symmetric的

令$A^\top A = V\Lambda V^\top$是$AA^\top$的一个特征值分解，其中

$$\begin{gather*} V\in\mathbb{R}^{n\times n}\quad {\rm s.t.}\quad V^\top V = VV^\top = I\\ \Lambda = {\rm diag}(\lambda_1,\cdots,\lambda_n)\in\mathbb R^{n\times n}\quad\text{是一个对角矩阵，其中}\lambda_1\geq\lambda_2\geq\cdots\geq \lambda_n \end{gather*}$$

1. 由于$A^\top A$是SPSD的，因此$\lambda_1\geq\lambda_2\geq\cdots\geq \lambda_n\geq 0$

2. $w_i$为$AV\in\mathbb R^{m\times n}$的第$i$列，则

   $$\begin{align*} w_i^\top w_j &= (AVe_i)^\top(AVe_j)=e_i^\top V^\top A^\top AVe_j\\ &=e_i^\top (V^\top V)\Lambda (V^\top V)e_j\\ &=\left\{\begin{aligned}&\lambda_i&&i=j\\&0&&i\neq j\end{aligned}\right. \end{align*}$$

   因此$AV$的列是正交的

3. 定义$\sigma_i = \|w_i\|_2 =\sqrt{w_i^\top w_i}= \sqrt{\lambda_i}$，$u_i=w_i/\|w_i\|_2$

   $$\begin{gather*} U = \begin{bmatrix}u_1&u_2&\cdots&u_n\end{bmatrix}\in\mathbb R^{m\times n}\\ \Sigma = {\rm diag}(\sigma_1,\cdots,\sigma_n)\in\mathbb R^{n\times n} \end{gather*}$$

   则$U^\top U=I(UU^\top\neq I~{\rm unless}~m=n)$，且$U\Sigma=[w_1,\cdots,w_n]=AV$

   $\rightarrow A = U\Sigma V^\top$

综上，$A = U\Sigma V^\top$，定义$p=\min\{m,n\}$其中

$$\begin{gather*} U\in\mathbb R^{m\times p}~{\rm s.t.}~U^\top U =I\\ V\in\mathbb R^{p\times p}~{\rm s.t.}~V^\top V=I\\ \Sigma\in\mathbb R^{n\times p}~\text{是一个对角矩阵满足}~\sigma_1\geq \sigma_2\geq\cdots\geq\sigma_n\geq0\\ \end{gather*}$$

properties of SVD

1. $$\begin{gather*}\left\{\begin{aligned}AV &= U\Sigma\\A^\top U&=V\Sigma\end{aligned}\right.\\ \left\{\begin{aligned}Av_i &= \sigma_i u_i\\A^\top u_i&=\sigma_iv_i\end{aligned}\right. \end{gather*}$$

2. $$\left\{\begin{aligned}A^\top Av_i &= \sigma_i^2v_i\\AA^\top u_i&=\sigma_i^2u_i\end{aligned}\right.$$

3. SVD是矩阵分析中有用的工具

   • ${\rm rank}(A)=$ 非零特征值数量

   • ${\rm Ran}(A)={\rm span}(u_1,\cdots,u_r)$，其中$r={\rm rank}(A)$

     proof

     $$\begin{align*} {\rm Ran}(A)&=\{A\mathbf{x}|\mathbf{x}\in\mathbb{R}^{n}\}=\{U\Sigma V^{T}\mathbf{x}\big|\mathbf{x}\in\mathbb{R}^{n}\}\\ &=\left\{\sum_{i=1}^{p}\sigma_{i}u_{i}(v_{i}^{T}\mathbf{x})\big|\mathbf{x}\in\mathbb{R}^{n}\right\}\\ &=\left\{\sum_{i:\sigma_i\neq 0}\sigma_{i}(v_{i}^{T}\mathbf{x})\cdot u_{i}|\mathbf{x}\in\mathbb{R}^{n}\}={\rm span}\{u_{1},u_{2},\ldots,u_{r}\}\right\} \end{align*}$$

   • ${\rm Ker}(A)={\rm span}\{v_1,v_2,\cdots,v_r\}^{\perp}$

   • $\|A\|_2 =\sigma_1,~\|A\|_F = \sqrt{\sum_{i=1}^p \sigma_i}$

     proof

     $$\begin{align*} \|A\|_{2}&=\max_{\|x\|_{2}=1}\|Ax\|_{2}=\left(\max_{\|x\|_{2}=1}\|Ax\|_{2}^{2}\right)^{1/2}=\left(\max_{\|x\|_{2}=1}x^{T}A^{T}Ax\right)^{1/2}\\ &=\left(\max_{\|x\|_{2}=1}x^{T}V\Sigma ^2V^\top x\right)^{1/2}=\left(\max_{\|x\|_{2}=1}y^\top\Sigma ^2y\right)^{1/2}=(\sigma_{1}^{2})^{1/2}=\sigma_{1} \end{align*}$$

     由于$V$是正交矩阵，因此$\|V^\top x\|=1$

     $$\begin{align*} \|A\|_{F}&=\left(\langle A,A\rangle\right)^{1/2}=\left(\langle U\Sigma V^{\top},U\Sigma V^{\top}\rangle\right)^{1/2}\\ &=\left({\rm tr}(V\Sigma U^{\top}U\Sigma V^{\top})\right)^{1/2}=\left({\rm tr}(V\Sigma^{2}V^{T})\right)^{1/2}=\left({\rm tr}(\Sigma^{2}V^{\top}V)\right)^{1/2}\\ &=\left({\rm tr}(\Sigma^{2})\right)^{1/2}=(\sigma_{1}^{2}+\sigma_{2}^{2}+\cdots+\sigma_{p}^{2})^{1/2}. \end{align*}$$

   • 几何意义

     

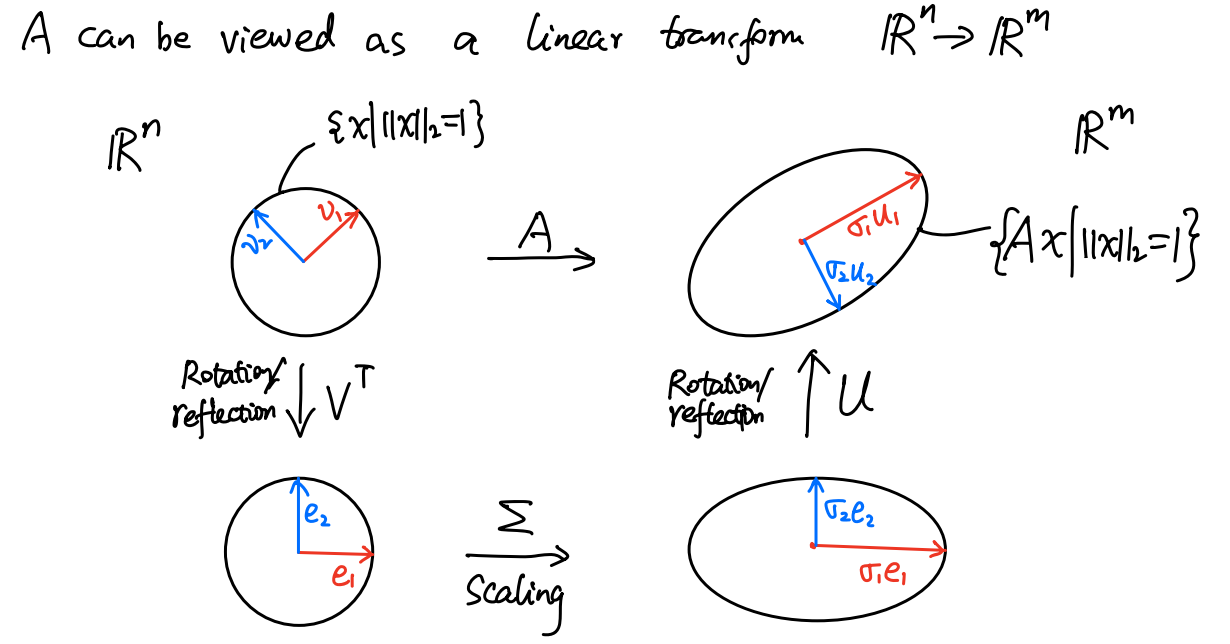
4. SVD是关于一个矩阵的最优的低秩近似

   $A\in\mathbb{R}^{m\times n}, A = U\Sigma V^\top$，则可以将$A$表示为：

   $$A = \sum_{i=1}^p\sigma_iu_iv_i^\top$$

   令$k$是一个正整数满足$k\leq p$，定义

   $$A_k = \sum_{i=1}^k\sigma_iu_iv_i^\top$$

   则

   $$\begin{gather*} A_k = \operatorname*{argmin}_{B:{\rm rank}(B)\leq k}\|A-B\|_2\\ A_k = \operatorname*{argmin}_{B:{\rm rank}(B)\leq k}\|A-B\|_F \end{gather*}$$

   proof: 2-norm case

   $$\|A-A_k\|_2 = \left\|\sum_{i=1}^p\sigma_iu_iv_i^\top-\sum_{i=1}^k\sigma_iu_iv_i^\top\right\|_2=\left\|\sum_{i=k+1}^p\sigma_iu_iv_i^\top\right\|_2=\sigma_{k+1}$$

   接下来希望证明对于任意$B:{\rm rank}(B)\leq k$有

   $$\|A-B\|_2\geq \sigma_{k+1}$$

   不妨设$p=n\quad ({\rm i.e.}\quad n\leq m)$。由于${\rm rank}(B)\leq k$，

   $${\rm rank}(B[v_1,\cdots,v_{k+1}])\leq {\rm rank}(B)\leq k$$

   因此

   $$B\underbrace{\begin{bmatrix}v_1&v_2&\cdots&v_{k+1}\end{bmatrix}\begin{bmatrix}c_1\\c_2\\\vdots\\c_{k+1}\end{bmatrix}}_{\text{define}~ w}=0$$

   存在一个非0解。不妨设$\|w\|_2 = 1\quad ({\rm i.e.}\quad \sum_{i=1}^{k+1}c_i^2=1)$

   $$\begin{align*} \|A-B\|^2_2 &\overset{(1)}{\geq} \|(A-B)w\|_2^2=\|Aw\|_2^2=\left\|\sum_{i=1}^{k+1}c_iAv_i\right\|_2^2\\ &\overset{(2)}{=}\left\|\sum_{i=1}^{k+1}c_i\sigma_iu_i\right\|_2^2\overset{(3)}{=}\sum_{i=1}^{k+1}c_i^2\sigma_i^2\geq \sum_{i=1}^{k+1}c_i^2\sigma_{k+1}^2=\sigma_{k+1^2} \end{align*}$$

   其中(1)使用了$\|AB\|_2\leq\|A\|_2\|B\|_2$

   (2)使用了SVD的性质1

   (3)成立是因为$U$的列向量是正交的

   $$\left\|\sum_{i=1}^{k+1}c_i\sigma_iu_i\right\|_2^2=\sum_{i=1}^{k+1}\sum_{j=1}^{k+1}c_ic_j\sigma_i\sigma_j\langle u_i,u_j\rangle$$

Application

$$A\approx LR^\top$$

其中$L\in\mathbb R^{m\times k}$，$R\in\mathbb R^{k\times n}$。

PCA

$$\min_{L\in\mathbb R^{m\times k},R\in\mathbb{R}^{n\times k}}\|A-LR^\top\|_F^2\Leftrightarrow \min_{M:{\rm rank}(M)\leq k}\|A-M\|_F^2$$

The solution is given by $k$-truncated SVD of A

Column Subset Selection

$L$: $A$的一些列，$R\in\mathbb R^{n\times k}$

$$\min_{\begin{gathered}L:k-\text{columns of }A\\R\in\mathbb{R}^{n\times k}\end{gathered}}\|A-LR^\top\|_F^2\Leftrightarrow \min_{\begin{gathered}S\sub\{1,\cdots,m\}\\|S|=k\\R\in\mathbb{R}^{n\times k}\end{gathered}}\|A-A_sA_s^{\dagger}A\|_F^2$$

PRQR gives a good approximate solution

Non Negtive Matrix Factorization

$$\min_{\begin{gathered}L\in\mathbb{R}^{m\times k}_+\\R\in\mathbb{R}^{k\times n}_+\end{gathered}}\|A-LR^\top\|_F^2$$

to be continue.