封面：Apriori Algorithm in Machine learning | by Palak Bhandari | Medium

问题定义

考虑以下表格，横轴为物品，纵轴为数据，

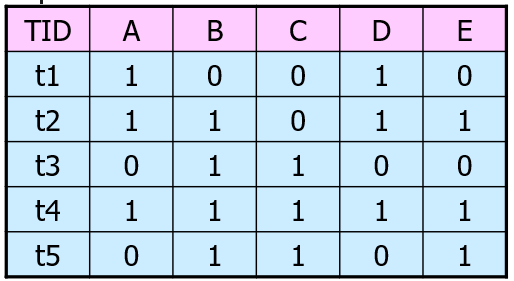
image-20250309164907738

首先定义以下概念：

  • item set: 一些物品的组合，例如{B,C}\{B,C\}
  • rule: 一个item set与另一个物品的关系，例如{B,C}→E\{B,C\}\rightarrow E表示顾客购买B,CB,C可以推断顾客会购买EE
  • support: support({B,C}→E)=∣{B,C,E}∣{\rm support}(\{B,C\}\rightarrow E)=|\{B,C,E\}|
  • confidence: support({B,C}→E)/∣{B,C}∣{\rm support}(\{B,C\}\rightarrow E)/|\{B,C\}|

我们希望寻找support和confidence大于某个阈值的关联规则

算法

initializek←1Lk={{item1},{item2},⋯ ,{itemn}}while Lk≠∅k←k+1Ck=∅Candidate GenerationJoin step: 将具有相同前缀的项进行合并将(pk−1,a),(pk−1,b)合并为(pk−1,a,b)Ck←{Ck,(pk−1,a,b)}Prune stepfor c∈Ck对于所有c的k−1子集s，如果其不在Lk−1中，则删除cLarge Itemset Generation统计每个itemset的count，然后选择大于threshold的itemsetend while\begin{align*} &\textbf{initialize}\\ &k\leftarrow 1\\ &L_k = \big\lbrace\lbrace\text{item1}\rbrace,\lbrace\text{item2}\rbrace,\cdots,\lbrace\text{itemn}\rbrace\big\rbrace\\ &\textbf{while } L_{k}\neq \varnothing\\ &\quad k\leftarrow k+1\\ &\quad C_k=\varnothing\\ &\quad \text{Candidate Generation}\\ &\quad \quad \text{Join step: 将具有相同前缀的项进行合并}\\ &\quad \quad\quad \text{将}(p_{k-1},a),(p_{k-1},b)\text{合并为}(p_{k-1},a,b)\\ &\quad\quad\quad C_k\leftarrow \{C_k,(p_{k-1},a,b)\}\\ &\quad \quad \text{Prune step}\\ &\quad\quad\quad\textbf{for }c\in C_{k}\\ &\quad\quad\quad\quad \text{对于所有}c\text{的}k-1\text{子集}s\text{，如果其不在}L_{k-1}\text{中，则删除}c\\ &\quad \text{Large Itemset Generation}\\ &\quad\quad \text{统计每个itemset的count，然后选择大于threshold的itemset}\\ &\textbf{end while} \end{align*}

example

IMG_1178