QR分解

Introduction

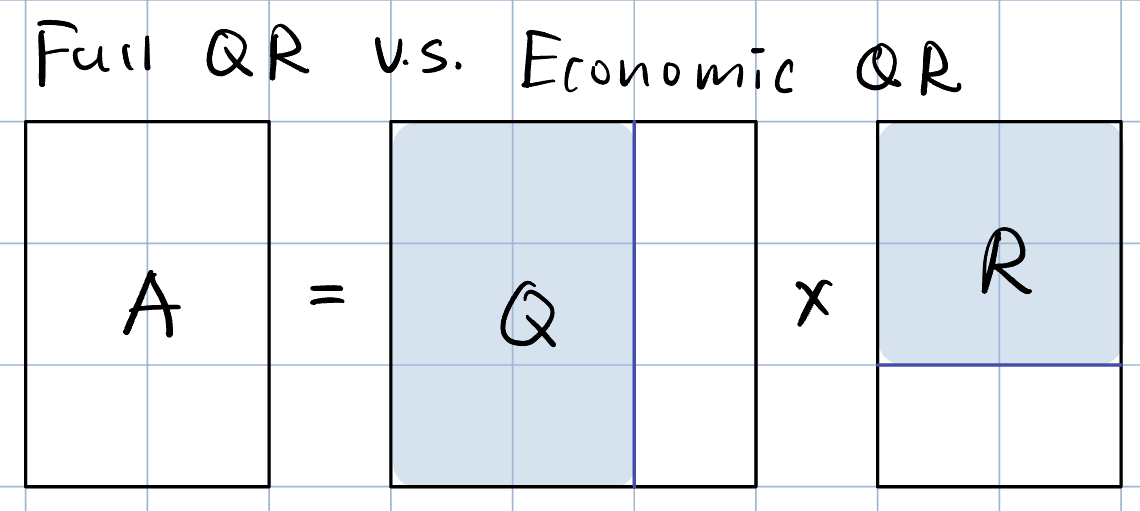
full QR

$A\in\mathbb R^{m\times n}\quad {\rm s.t.}~ m\geq n, ~{\rm rank}(A) = n$，则存在一个分解，使得

$$A =QR$$

其中，

$$\begin{gather*} Q\in\mathbb R^{m\times m}\text{ 是一个正交矩阵 }(Q^\top Q = QQ^\top = I)\\ R\in\mathbb{R}^{m\times n}\text{ 是一个上三角阵} \end{gather*}$$

Economic QR

$$\begin{gather*} Q\in\mathbb R^{m\times n}\text{ 是一个 }(Q^\top Q = I)\\ R\in\mathbb{R}^{n\times n}\text{ 是一个上三角阵(对角线非零)} \end{gather*}$$

Theorem

令

$$\begin{align} A &= \begin{bmatrix}a_1&\cdots&a_n\end{bmatrix}\\ Q &= \begin{bmatrix}q_1&\cdots&q_n&\cdots&q_m\end{bmatrix} \end{align}$$

对于任意$k=1,\cdots,n$, $\{q_1,\cdots,q_k\}$是${\rm span}\{a_1,\cdots,a_k\}$的一组正交基

proof

$\{q_1,\cdots,q_k\}$是一组基

$$\begin{align} \begin{bmatrix}a_1&\cdots&a_n\end{bmatrix}= \begin{bmatrix}q_1&\cdots&q_n\end{bmatrix} \begin{bmatrix}r_{11}&\cdots&r_{1k}\\&\ddots&\vdots\\&&r_{kk} \end{bmatrix} \end{align}$$

$$\begin{align} {\rm span}\{a_1,\cdots,a_k\} &= {\rm Range}(A)=\left\{\begin{bmatrix}a_1&\cdots&a_k\end{bmatrix}\mathbf{x}|\mathbf{x}\in\mathbb R^{k}\right\}\\ &= \left\{\begin{bmatrix}q_1&\cdots&q_k\end{bmatrix} \begin{bmatrix}r_{11}&\cdots&r_{1k}\\&\ddots&\vdots\\&&r_{kk}\end{bmatrix} \mathbf{x}\Bigg|\mathbf{x}\in\mathbb R^{k}\right\}\\ &= \left\{\begin{bmatrix}q_1&\cdots&q_k\end{bmatrix} \mathbf{y}\big|\mathbf{y}\in\mathbb R^{k}\right\} \end{align}$$

$\{q_1,\cdots,q_k\}$之间彼此正交

$$QQ^\top = I\Rightarrow\langle q_i,q_j\rangle = q_i^\top q_j=\left\{\begin{aligned}&1&&{\rm if }~i=j\\&0&&{\rm if }~i\neq j\end{aligned}\right.$$

得证。

Application

求解线性方程组

$$A\mathbf x=b\Leftrightarrow QR\mathbf x=b\Leftrightarrow R\mathbf x=Q^\top b$$

由于$R$是一个上三角阵，因此使用back substitution很容易求解

求解最小二乘

由于$Q$的列向量是${\rm Range}(A)$的一组正交基，因此$QQ^\top$是投影到${\rm Range}(A)$的一个正交投影，$(I-QQ^\top)$是投影到${\rm Range}(A)^\perp$的一个正交投影。

$$b=QQ^\top b+(I-QQ^\top)b$$

$$\begin{align} \|Ax-b\|_2^2 &= \|QRx-(QQ^\top b+(I-QQ^\top)b)\|_2^2\\ &=\|Q(Rx-Q^\top b)-(I-QQ^\top)b\|^2_2\\ &\overset{(1)}{=}\|Q(Rx-Q^\top b)\|_2^2+\|(I-QQ^\top)b\|^2_2\\ &=\|Q(Rx-Q^\top b)\|_2^2+C \end{align}$$

(1)成立是因为$Q(Rx-Q^\top b)\in{\rm Range}(Q)={\rm Range}(A)$, $(I-QQ^\top)b\in{\rm Range}(A)^\perp$，因此这两个向量正交。

$$\min_{x\in\mathbb R^n}\|Ax-b\|_2^2 \Leftrightarrow \min_{x\in\mathbb R^n}\|Rx-Q^\top b\|$$

$R$是一个上三角阵，因此新问题很好求解（back substitution）

Used as subroutines in other matrix computation algorithms, e,g, SVD, eigen value problems

Computation of QR decomposition

Gram Schmidt procedure (格拉姆-施密特正交化)

形式1

$$\beta_n = \alpha_n-\sum_{i=1}^{n-1}\frac{\langle \alpha_n,\beta_i\rangle}{\langle \beta_i,\beta_i\rangle}\beta_i$$

形式2

Householder QR algorithm

思路：一个正交阵的转置、逆矩阵是正交阵，两个正交阵的乘积是正交阵，使用一系列简单的正交阵逼近$Q$

$$\begin{align} Q_1A &= \begin{bmatrix}*&*&\cdots&*\\0&*&\cdots&*\\\vdots&\vdots&\ddots&\vdots\\0&*&*&*\end{bmatrix}\\ Q_2Q_1A &= \begin{bmatrix}*&*&*&\cdots&*\\0&*&*&\cdots&*\\0&0&*&\cdots&*\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&*&*&*\end{bmatrix}\\ \end{align}$$

使用 Householder transform 来构建$Q_i$

Householder Transform

Definition

$u,v\in\mathbb R^{m}$ 满足$\|u\|_2=\|v\|_2$，Householder Transform matrix $H_{u,v}$定义为：

$$H_{u,v} = I-2ww^\top,\quad \text{where } w = \frac{u-v}{\|u-v\|_2}$$

性质

$$\begin{align} H_{u,v}^\top = H_{u,v} \quad &H_{u,v}\text{ is symmetric}\\ H_{u,v}^\top H_{u,v} = H_{u,v}H_{u,v}^\top = I\quad &H_{u,v}\text{ is square orthogonal}\\ H_{u,v}v = u\quad \text{ and }\quad &H_{u,v}u=v \end{align}$$

proof of property 2

$$\begin{align} (I-2ww^\top)^\top(I-2ww^\top)&=(I-2ww^\top)(I-2ww^\top)\\ &=I-4ww^\top+4w(w^\top w)w^\top\\ &\overset{(2)}{=}I \end{align}$$

(2)成立是因为$w^\top w=1$

proof of property 3

由于$\|u\|=\|v\|$

$$\begin{gather*} (u-v)^\top(u+v)=\|u\|^2-\|v\|^2+u^\top v-v^\top u=0\\ \Rightarrow u-v\perp u+v \end{gather*}$$

由于$w = \frac{u-v}{\|u-v\|_2}$, $ww^\top u = -ww^\top v$

$$\begin{gather*} ww^\top (u+v) = w\frac{(u-v)^\top}{\|u-v\|_2}(u+v)=0\\ \Rightarrow ww^\top u = -ww^\top v \end{gather*}$$

接下来证$(I-ww^\top)u = (I-ww^\top)v$

$$\begin{gather*} ww^\top (u-v) = u-v\\ \Rightarrow (I-ww^\top)(u-v) = 0\\ \Rightarrow (I-ww^\top)u = (I-ww^\top)v\\ \end{gather*}$$

因此有，

$$\begin{align} H_{u,v} v&=(I-2ww^\top)v = (I-ww^\top)v-ww^\top v\\ &=(I-ww^\top)u+ww^\top u = u \end{align}$$

相似地

$$\begin{align} H_{u,v} u&=(I-2ww^\top)u = (I-ww^\top)u-ww^\top u\\ &=(I-ww^\top)v+ww^\top v = v \end{align}$$

Algorithm

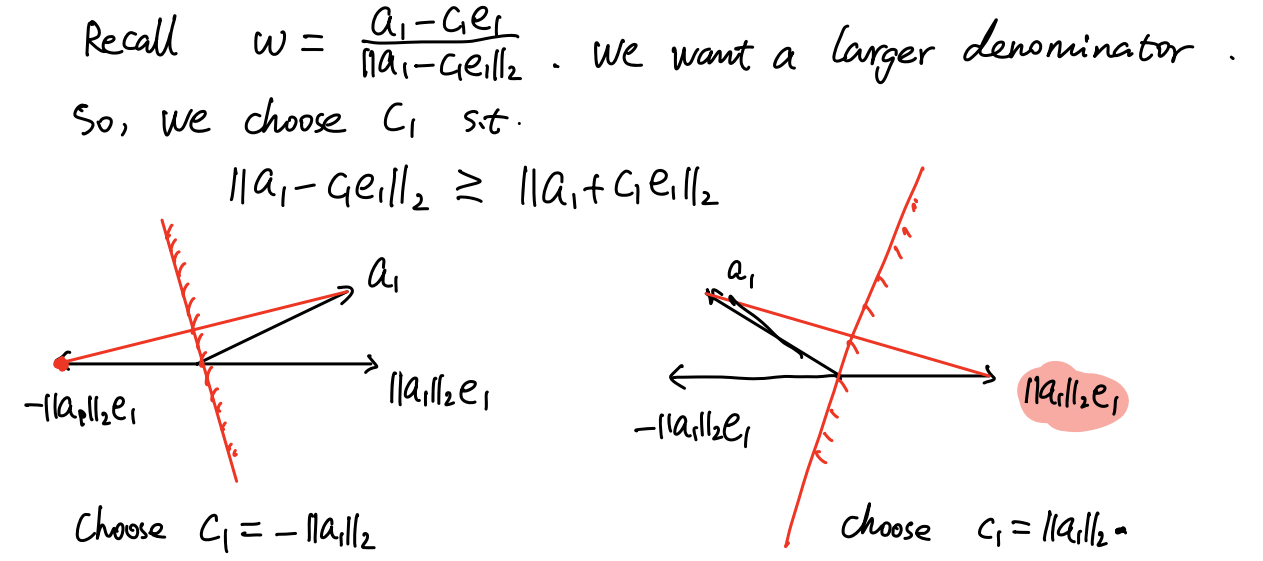
Recall that we want

$$\begin{align} Q_1A &= \begin{bmatrix}*&*&\cdots&*\\0&*&\cdots&*\\\vdots&\vdots&\ddots&\vdots\\0&*&*&*\end{bmatrix} \end{align}$$

取$Q_1a_1 = H_{a_1,c_1e_1}$

$c_1$的选取：
首先我们需要：

$$\|a_1\|_2 = \|c_1e_1\|_2\Rightarrow c_1=\left\{\begin{align}&\|a_1\|_2\\-&\|a_1\|_2\end{align}\right.$$

为了避免数值精度问题，希望分母上的数更大，因此选择$c_1=\|a_1\|_2$

$$\begin{align} Q_1A&=\begin{bmatrix}Q_1A_1&Q_1A[:,2:n]\end{bmatrix}\\ &=\begin{bmatrix}c_1e_1&(I-2w_1w_1^\top)A[:,2:n]\end{bmatrix}\\ &=\begin{bmatrix}c_1&\\0&\\\vdots&A[:,2:n]-2w_1w_1^\top A[:,2:n]\\0\end{bmatrix}\\& \equiv A^{(1)} \end{align}$$

以此类推，在第$k$步有：

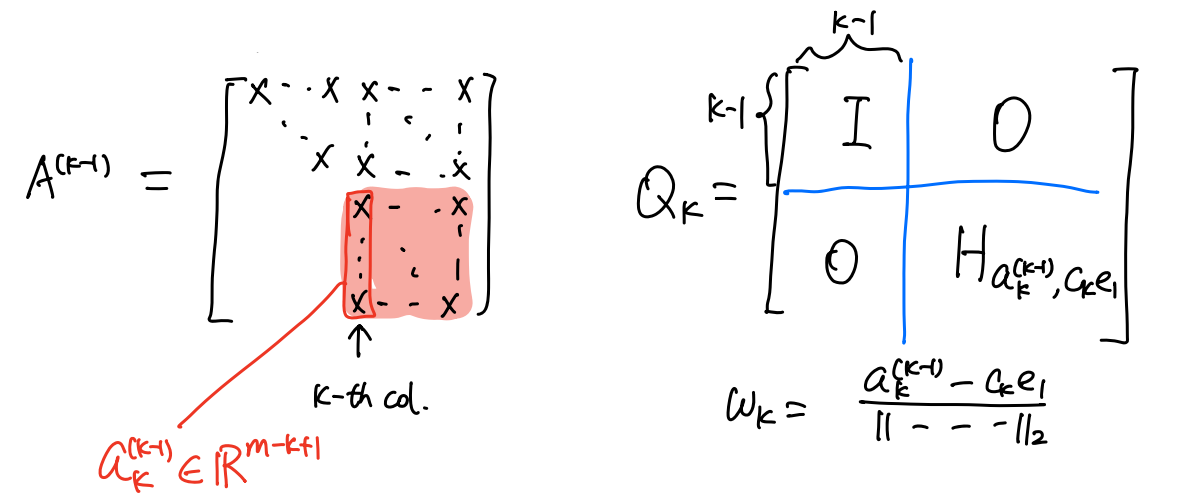
计算复杂度

如果只计算$R$和$w_1,\cdots w_n$ 而不显式地计算$Q$

$$\sum_{k=1}^n\mathcal{O}(m-k+1)(n-k)=\mathcal{O}(mn^2)$$

在第$k$步时，剩余矩阵大小为$(m-k+1,n-k+1)$，需要计算的部分为$(m-k+1,n-k)$（第一列不用计算，结果已知）

如果要计算full QR 中的$Q$，则还要计算

$$Q = Q_1Q_2\cdots Q_nI$$

计算复杂度为$\mathcal O(m^2n)$

如果只需要$Q$的前$n$列，则需要计算

$$Q[:,1:n] = Q_1Q_2\cdots Q_nI[:,1:n]$$

计算复杂度为$\mathcal O(mn^2)$

code

import numpy as np


def H(x, y):
    w = (x - y) / np.linalg.norm(x - y)
    return np.eye(x.shape[0]) - 2 * w @ w.T


def QR(A):
    # Initialize Q
    Q = np.eye(A.shape[0])
    for k in range(A.shape[0]):
        # Compute H_k
        a_k = A[k:, k:k + 1]
        a_k_norm = np.linalg.norm(a_k)
        e_k = np.zeros_like(a_k)
        e_k[0, 0] = 1
        # Choose c_k
        if np.linalg.norm(a_k - a_k_norm * e_k) >= np.linalg.norm(a_k + a_k_norm * e_k):
            c_k = a_k_norm
        else:
            c_k = -a_k_norm
        H_k = H(a_k, c_k * e_k)
        # Compute R/ Update A
        A[k:, k:] = H_k @ A[k:, k:]
        # Update Q
        Q_k = np.eye(A.shape[0])
        Q_k[k:, k:] = H_k
        Q = Q@Q_k
    return Q, A


A = np.array([[0, 3, 1], [0, 4, -2], [2, 1, 1]],dtype=np.float64)

Q, R = QR(A)

Given’s rotation QR algorithm

思路：

$$\begin{gather*} \begin{bmatrix}1&&&\\&1&&\\&&c&s\\&&-s&c\end{bmatrix}\begin{bmatrix}\times&\times&\times\\\times&\times&\times\\\times&\times&\times\\\times&\times&\times\end{bmatrix}=\begin{bmatrix}\times&\times&\times\\\times&\times&\times\\\times&\times&\times\\0&\times&\times\end{bmatrix}\\ \begin{bmatrix}1&&&\\&c&s&\\&-s&c&\\&&&1\end{bmatrix}\begin{bmatrix}\times&\times&\times\\\times&\times&\times\\\times&\times&\times\\0&\times&\times\end{bmatrix}=\begin{bmatrix}\times&\times&\times\\\times&\times&\times\\0&\times&\times\\0&\times&\times\end{bmatrix} \end{gather*}$$

假设要将$[a,b]^\top$中的$b$变为0，则

$$c=\frac{a}{\sqrt{a^2+b^2}}\quad s=\frac{b}{\sqrt{a^2+b^2}}$$

code

def GivensRotation(A):
    G = np.eye(A.shape[0])
    for i in range(A.shape[1]):
        for j in range(A.shape[0] - 1, i, -1):
            c = A[j - 1, i] / np.sqrt(A[j - 1, i] ** 2 + A[j, i] ** 2)
            s = A[j, i] / np.sqrt(A[j - 1, i] ** 2 + A[j, i] ** 2)
            G_ij = np.eye(A.shape[0])
            G_ij[j - 1:j + 1, j - 1:j + 1] = np.array([[c, s], [-s, c]])
            A[j - 1:j + 1, :] = G_ij[j - 1:j + 1, j - 1:j + 1] @ A[j - 1:j + 1, :]
            G = G_ij @ G
    return G.T, A

Rank Revealing QR

只做简要介绍，无算法

Definition

存在$P,Q,R,r$ 满足$AP=QR$

其中

$$\begin{gather*} P\in\mathbb R^{n\times n}\quad \text{is a permutation on columns of }A\\ r\in\mathbb R \quad \text{numerical rank}\\ Q = [Q_1, Q_2]\quad\text{s.t.}~QQ^\top=Q^\top Q=I\\ R = \begin{bmatrix}R_{11}&R_{12}\\0&R_{22}\end{bmatrix}\quad R_{11}\text{是一个上三角阵，}R_{22}\text{相比于}R_{11}\text{ norm很小} \end{gather*}$$

接下来证明$\{\tilde{a}_1,\cdots,\tilde{a}_r\}$是$A$的representative columns

$$\begin{gather*} AP=[\tilde{a}_1,\cdots,\tilde{a}_n]\\ \Rightarrow AP=[\tilde{a}_1,\cdots,\tilde{a}_r,\tilde{a}_{r+1},\cdots\tilde{a}_n]=[Q_1,Q_2]\begin{bmatrix}R_{11}&R_{12}\\&R_{22}\end{bmatrix}\\ =[Q_1R_{11},Q_1R_{12}+Q_2R_{22}] \overset{(3)}{\approx}[Q_1R_{11},Q_1R_{12}] \end{gather*}$$

(3)成立是因为$R_{22}\approx 0$

$$\begin{gather*} {\rm Range}(A)={\rm Range}(AP)\approx{\rm Range}(Q_1[R_{11},R_{12}])\\ ={\rm Range}(Q_1)={\rm Range}([\tilde{a}_1,\cdots,\tilde{a}_n]) \end{gather*}$$

$${\rm span}([\tilde{a}_1,\cdots,\tilde{a}_n])\approx {\rm span}([\tilde{a}_1,\cdots,\tilde{a}_r])$$