封面:Epsilons, no. 3: The LU decomposition - by Tivadar Danka
Definition
考虑A∈Rn×n,满足所有顺序主子式(leading principal minors)不为0,则存在以下分解:
A=LU
其中,L∈Rn×n是一个单位下三角矩阵,U∈Rn×n是一个上三角阵
L=1l1,2⋮ln,11⋮ln,2⋱⋯01U=u1,10⋯⋱u1,n−1⋮un−1,n−1u1,n⋮un−1,nun,n
Application
1. 解线性方程
对于线性方程组Ax=b, A∈Rn×n,x∈Rn,b∈Rn. 如果有A=LU,则
Ax=b⇔LUx=b⇔{UxLy=y=b
由于L是一个下三角阵,可以轻松的得到Ly=b的解
Ly=b⇔1l21l31⋮ln11l32⋮ln21⋱⋯⋱lnn−11y1y2y3⋮yn=b1b2b3⋮bn
按照y1→yn的顺序:
y1=b1l21y1+y2=b2⋮ln1y1+⋯+lnn−1yn−1+yn=bn
对于yk,y1:k−1都是已知的,每个方程只有yk一个未知数。
由于U是一个上三角矩阵,同样的,可以很轻松的得到Ux=y的解
ux=y⇔u1,1⋯⋱⋯⋱un−1,n−1u1,n⋮un−1,nun,nx1⋮xn−1xn=y1⋮yn−1yn
从xn→x1的顺序。
2. 计算行列式
det(A)=det(LU)=det(L)det(U)=i=1∏nuii
Algorithm
思路:通过一系列简单的矩阵变换,逐步将A转化为上三角矩阵U。在每一步中,使用一个单位下三角矩阵Lj来消去A中的部分元素,直到得到最终的U矩阵。
A=LU⇔L−1A=U⇔Ln−1⋯L2L1A=U
其中,L1:n−1都是简单的单位下三角阵
令
Lj=I−liej⊤
其中,lj满足lij=0,i≤j
lj=0⋮0lj+1,j⋮ln,j,ej⊤=[0⋯01j↓ 0⋯0]
Lj=I−ljej⊤=1⋱11−lj+1,j⋮−ln,j⋱⋱1
令ai和a~i分别表示A的第i列和第i行
A=[a1⋯an]=a~1⋮a~n
希望经过L1的变换之后,a1这一列可以变成一个上三角阵的形状(a1,2:n=0)
L1a1=c1e1, for some c1∈R
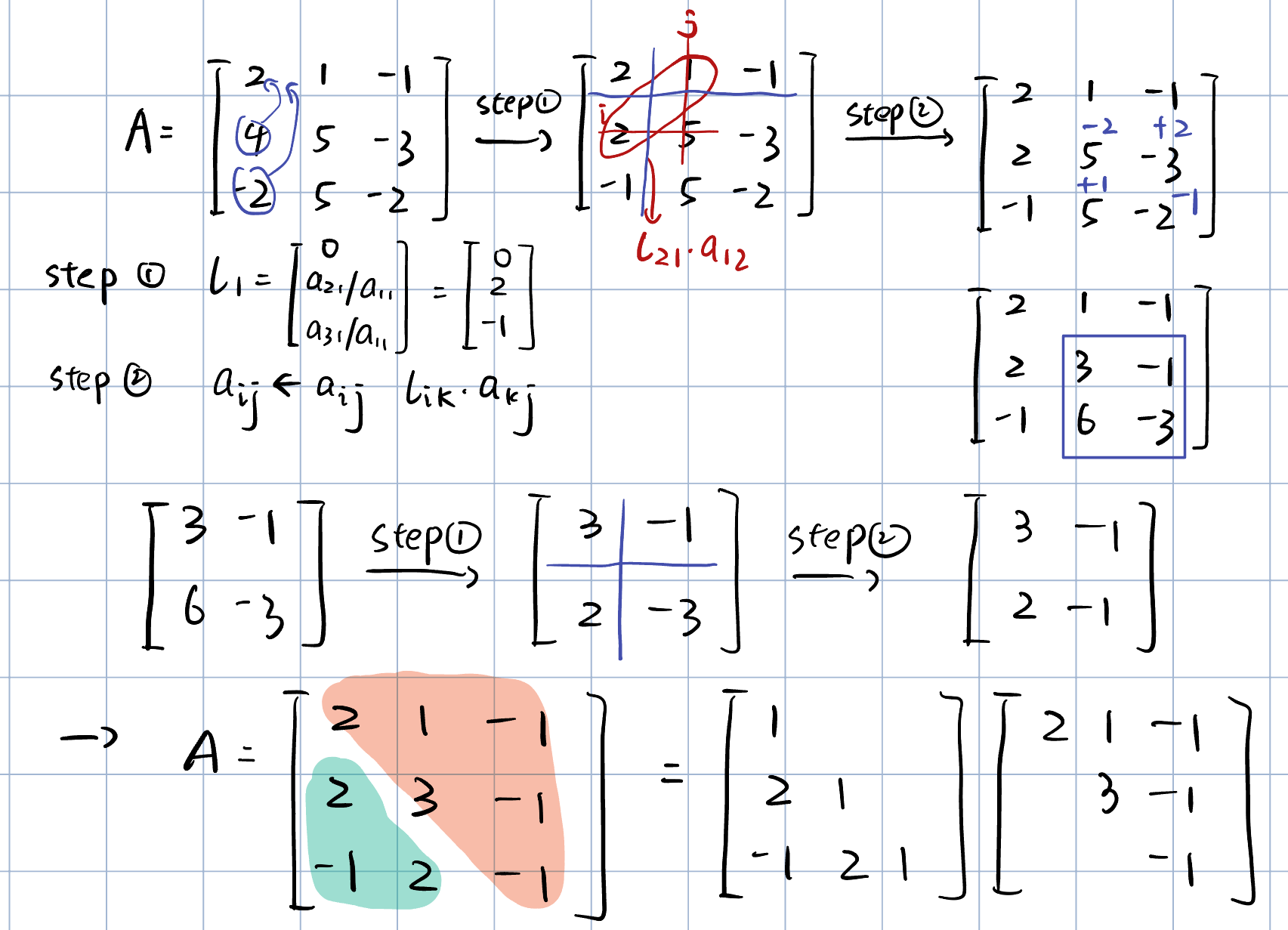
(I−l1e1⊤)a1=c1e1⇒a1−l1(e1⊤a1)=c1e1⇔a1−a11l1=c1e1⇔a11a21⋮an1−0a11l21⋮a11ln1=c10⋮0
选择
l1=0a21/a11⋮an1/a11
A(1)=L1A=(I−l1e1⊤)A=A−l1a~1=A−0l21⋮ln1[a11a12⋯a1n]=a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann−0l21a11⋮ln1a110⋯li1⋅a1j0=a110⋮0a12⋯aij−li1a1ja1n
对于L2,类似的,只需要解一个n−1维的子问题
对于Lk和Ak−1
likaij(k)=aik(k−1)/akk(k)=aij(k−1)−likakj(k−1)
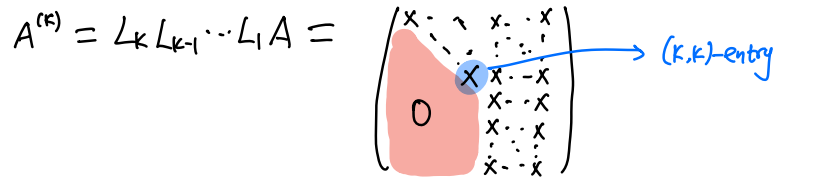
重复以上步骤直到k=n−1,最终,有:
Ln−1Ln−1⋯L2L1A=A(n−1)≡U
L=(Ln−1Ln−1⋯L2L1)−1
Theorem:
L=I+l1e1⊤+⋯+ln−1en−1⊤
proof:
L=L1−1⋯Ln−1−1
首先证明Lj−1=I+ljej⊤,recall that Lj=I−ljej⊤
(I+ljej⊤)(I−ljej⊤)=I−ljej⊤ljej⊤=I−lj(ej⊤lj)ej=I−0=I
根据定义 lj的第 j位是 0,而 ej只有第 j位是1,因此内积为0
然后使用归纳法:
L1−1L2−1=(I+l1e1⊤)(I+l2e2⊤)=I+l1e1⊤+l2e2⊤+l1e1⊤l2e2⊤=I+l1e1⊤+l2e2⊤+l1(e1⊤l2)e2⊤=I+l1e1⊤+l2e2⊤
和前面同样的道理
如果L1−1⋯Lk−1=I+l1e1⊤+⋯+lkek⊤,则
L1−1⋯Lk+1−1=(I+l1e1⊤+⋯+lkek⊤)(I+lk+1ek+1⊤)=I+l1e1⊤+⋯+lkek⊤+lk+1ek+1⊤+l1(e1⊤lk+1)ek+1⊤+⋯+lk(ek⊤lk+1)ek+1⊤=I+l1e1⊤+⋯+lkek⊤+lk+1ek+1⊤
检查L是不是单位上三角阵:
[L]ij=ei⊤Lej=ei⊤(I+l1e1⊤+⋯+ln−1en−1⊤)ej=Iij+ei⊤lj(ei⊤ej=0 if i=j)=⎩⎨⎧1+0=10+0=00+lij=lijif i=jif i<jif i>j
因此
L=1l21l31⋮ln11l32⋮ln21⋱⋯⋱lnn−11
最终算法


计算复杂度
k=1∑n−1((n−k)+2(n−k)2)=k′=1∑n−1(k′+2(k′)2)=O(n3)
Example
A=24−2155−1−3−2
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| import numpy as np
def LU(A):
assert A.shape[0] == A.shape[1]
for k in range(A.shape[0] - 1):
l = np.zeros((A.shape[1], 1))
l[k + 1:, 0] = A[k + 1:, k] / A[k, k]
A[k + 1:, k + 1:] = A[k + 1:, k + 1:] - l[k + 1:, :] @ A[k:k + 1, k + 1:]
A[k + 1:, k:k + 1] = l[k + 1:, :]
L = np.tril(A, k=-1) + np.eye(A.shape[0])
U = np.triu(A, k=0)
return L, U
A = np.array([[2, 1, -1], [4, 5, -3], [-2, 5, -2]])
L, U = LU(A)
print(L @ U)
|
变体
Pivoted LU decomposition
在LU分解中,有可能遇到akk=0的情况,此时算法无法继续。Pivoted LU decomposition 引入主元,即n−k+1矩阵左上角的元素。每次通过行交换选择最大的元素作为主元。使用矩阵P记录行交换过程,即
PA=LU
最终再交换回去。
同理可以进行列交换
PAQ=LU
Cholesky分解
Theorem:
如果A∈Rn×n是一个半正定矩阵,则存在一个分解:
A=LL⊤
其中L是一个下三角矩阵(不一定是单位下三角)
proof:
因为A时一个半正定矩阵,因此所有的顺序主子式都可逆。所以存在一个LU使得A=L0U
令D=diag(U),D可逆(我们假设主元不为0,这样的话U的对角线元素中也不会有0)
A=L0U=LD(D−1U)=L0DU0
其中U0是一个单位上三角阵。且U0=L0⊤,因为:
A⊤=A⇒U0⊤DL0=L0DU0L0−1U0⊤D=DU0L0−⊤
其中,L0−1U0⊤是一个下三角阵,U0L0−⊤是一个上三角阵
上三角阵的逆是上三角阵,下三角阵的逆是下三角阵
因此L0−1U0⊤和U0L0−⊤是对角阵(一个上三角阵等于一个下三角阵)。因此L0−1U0⊤=U0L0−⊤=I⇒U0=L0⊤
因此
A=L0DL0⊤
接下来证明dii>0:
令x=L0−⊤ei=0
x⊤Ax=ei⊤L0−1(L0DL0⊤)L−⊤ei=ei⊤Dei=dii>0
令
D1/2=d11⋮0⋯⋱⋯0⋮dnn
L=L0D1/2
A=L0D1/2D1/2L0⊤=LL⊤
Algorithom

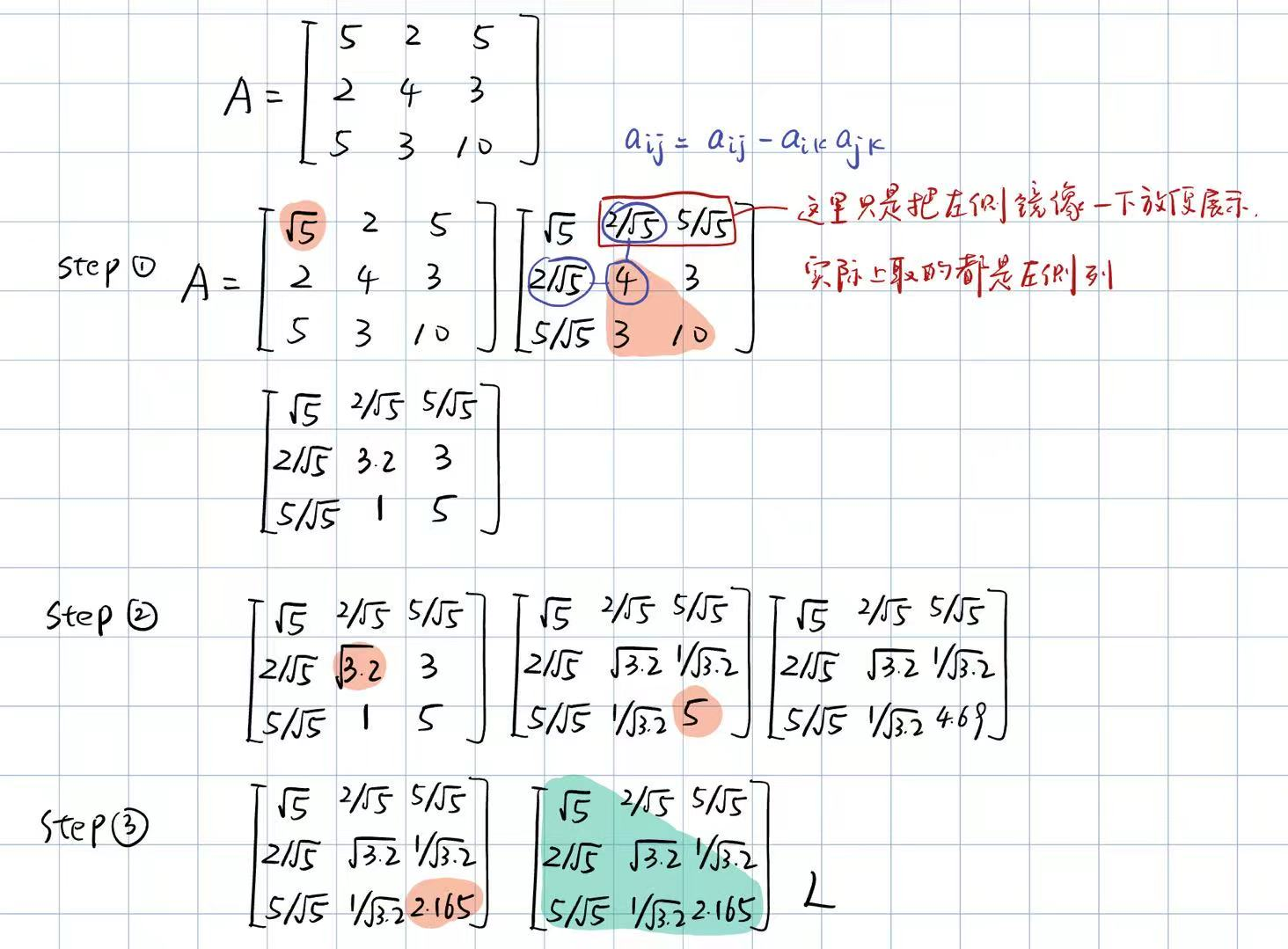
由于L=L0D21,因此在每一步都把l乘一个uii就可以了。
由于L0=U0因此在第二个for循环中只需要计算一半。
之所以第二个循环j=i to n部分要用ajk或ljk是因为A(1)=L1A=(I−l1e1⊤)A=A−l1a~1中L1发生了变化,在Cholesky分解中,L大概长这样,所以之前的一些性质失效了。
Li:=Ii−1000ai,iai,i1bi00In−i,
现在的算法基于以下事实:
A(i)=Ii−1000ai,ibi0bi∗B(i),A(i+1)=Ii−10001000B(i)−ai,i1bibi∗,A(i)=LiA(i+1)Li∗
Example
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def Cholesky_Decomposition(A):
assert A.shape[0] == A.shape[1]
for k in range(A.shape[0] - 1):
l = np.zeros((A.shape[1], 1))
A[k,k] = np.sqrt(A[k,k])
l[k + 1:, 0] = A[k + 1:, k] / A[k, k]
A[k + 1:, k + 1:] = A[k + 1:, k + 1:] - l[k + 1:, :] @ l[k+1:,:].T
A[k + 1:, k:k + 1] = l[k + 1:, :]
A[-1,-1] = np.sqrt(A[-1,-1])
L = np.tril(A, k=0)
U = np.triu(A, k=0)
return L, U
A = np.array([[5, 2, 5], [2, 4, 3], [5, 3, 10]],dtype=np.float64)
L, U = Cholesky_Decomposition(A)
|