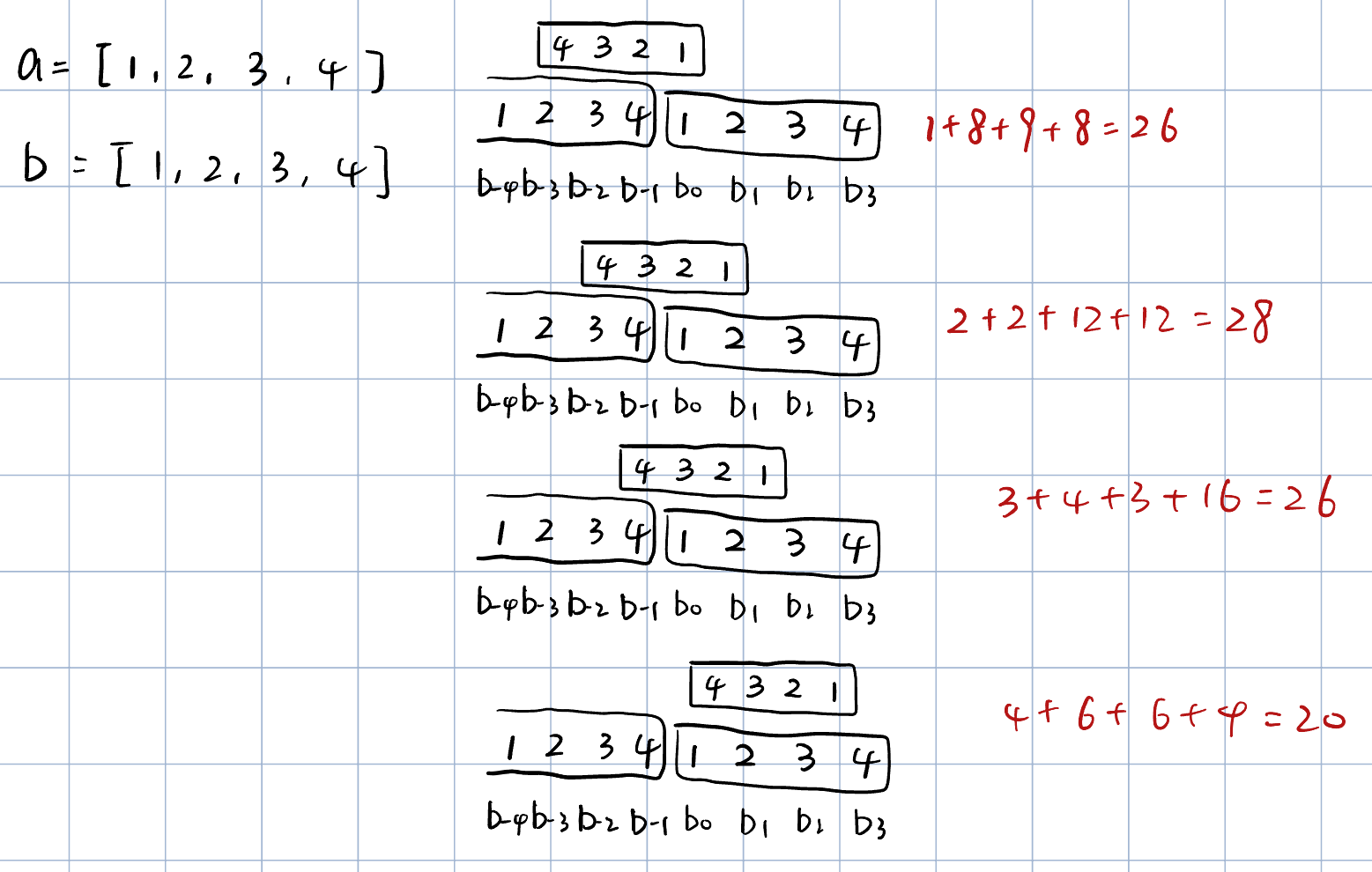Discrete Convolution

给定两个向量，f∈R2n+1,g∈R2m+1f\in\mathbb R^{2n+1},g\in\mathbb R^{2m+1}

f=[f−n,⋯ ,f−1,f0,f1,⋯ ,fn]g=[g−n,⋯ ,g−1,g0,g1,⋯ ,gn]\begin{gather} f = [f_{-n},\cdots,f{-1},f_0,f_1,\cdots,f_n]\\ g = [g_{-n},\cdots,g_{-1},g_0,g_1,\cdots,g_n] \end{gather}

其卷积f∗g∈R2(m+n)+1f*g\in\mathbb{R}^{2(m+n)+1}为：

(f∗g)k=∑i=−nnfigk−ifor k=−(m+n),⋯ ,−1,0,1,⋯(m+n)(f*g)_k = \sum_{i=-n}^nf_ig_{k-i}\quad \text{for }k=-(m+n),\cdots,-1,0,1,\cdots(m+n)

或者可以表示为：

(f∗g)k=∑i=−nn∑j=−mmfigjs.t. i+j=k(f*g)_k = \sum_{i=-n}^n\sum_{j=-m}^mf_ig_j\quad \text{s.t. } i+j=k

Example

离散卷积 example

性质

  1. f∗g=g∗ff*g=g*f
  2. f∗(g∗h)=(f∗g)∗hf*(g*h)=(f*g)*h
  3. f∗(g+h)=f∗g+f∗hf*(g+h)=f*g+f*h
  4. 令δ=[1]\delta = [1]，则f∗δ=ff*\delta =f

计算复杂度

  • 如果n≤mn\leq m，共有2(m+n)+12(m+n)+1个元素，每个元素要计算nn次，计算复杂度为O((m+n)n)\mathcal O((m+n)n)
  • 如果n>mn>m，相似的，计算复杂度为O((m+n)m)\mathcal O((m+n)m)

因此计算复杂度为O((m+n)min⁡{m,n})\mathcal O((m+n)\min\{m,n\})

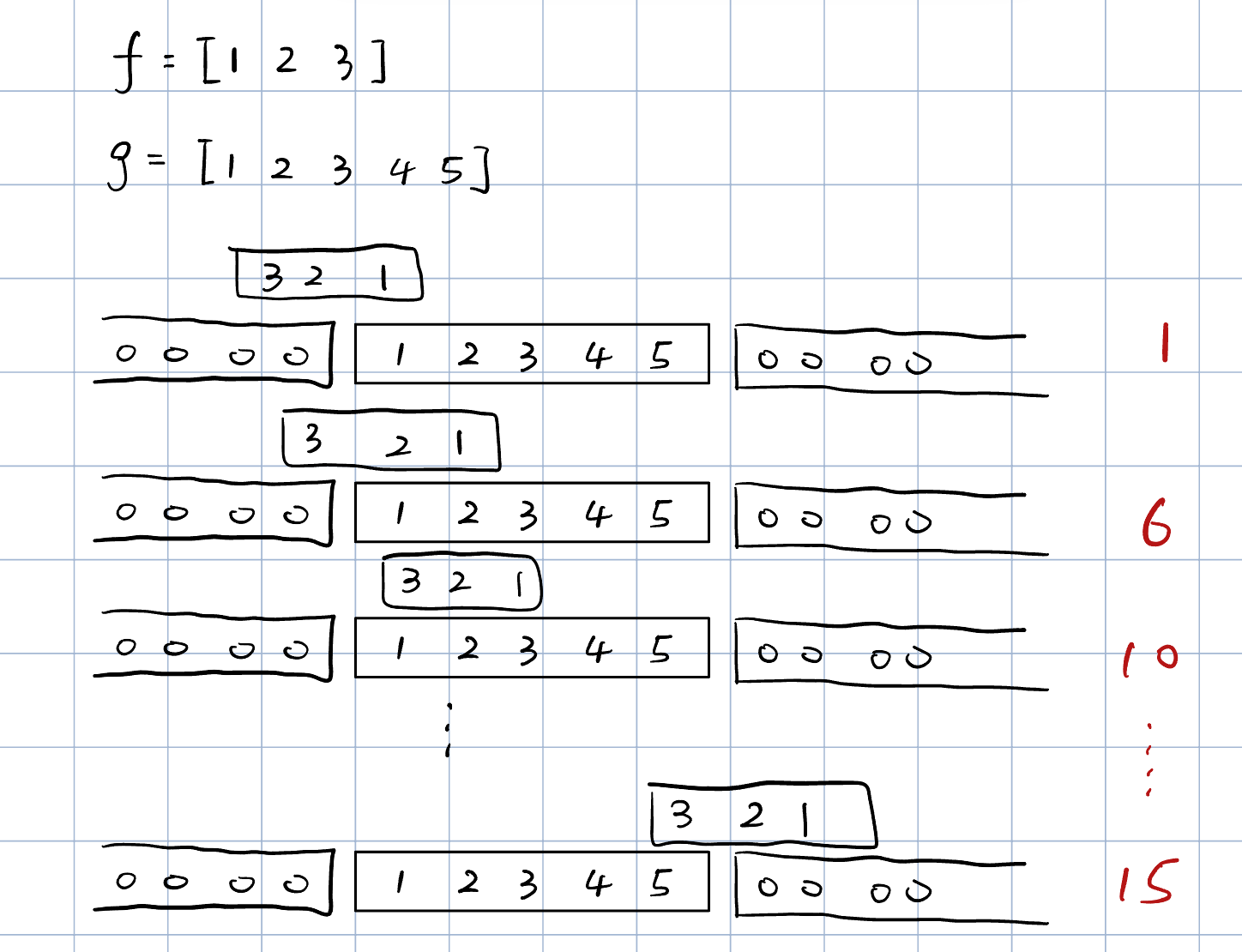
Circular Convolution

给定

a=[a0,⋯ ,aN−1]⊤∈RNb=[b0,⋯ ,bN−1]⊤∈RN\begin{align*} a &= [a_0,\cdots,a_{N-1}]^\top \in \mathbb R^{N}\\ b &= [b_0,\cdots,b_{N-1}]^\top \in \mathbb R^{N}\\ \end{align*}

循环卷积定义为：

(a⊛b)k=∑l=0N−1albk−lfor k=0,1,⋯ ,N−1where bk−l=b(k−l)+Nif −N+1≤k−l≤−1\begin{gather} (a\circledast b)_k = \sum_{l=0}^{N-1}a_lb_{k-l}\quad \text{for } k=0,1,\cdots,N-1\\ \text{where } b_{k-l}=b_{(k-l)+N}\quad \text{if }-N+1\leq k-l\leq -1 \end{gather}

example

循环卷积 example

性质

  1. a⊛b=b⊛aa\circledast b=b\circledast a
  2. a⊛(b⊛c)=(a⊛b)⊛ca\circledast(b\circledast c)=(a\circledast b)\circledast c
  3. a⊛(b+c)=a⊛b+a⊛ca\circledast(b+c)=a\circledast b+a\circledast c

Theorem

对于任意f∈R2n+1,g∈R2m+1f\in\mathbb R^{2n+1},g\in\mathbb R^{2m+1}，可以将f∗gf*g转化为a⊛ba\circledast b

a=[f0,f1,⋯ ,fn,0,⋯ ,0⏞2m个0,f−n,⋯ ,f−2,f−1]b=[g0,g1,⋯ ,gm,0,⋯ ,0⏟2n个0,g−m,⋯ ,g−2,g−1]\begin{gather} a = [f_0,f_1,\cdots,f_n,\overbrace{0,\cdots,0}^{2m\text{个} 0},f_{-n},\cdots,f_{-2},f_{-1}]\\ b = [g_0,g_1,\cdots,g_m,\underbrace{0,\cdots,0}_{2n\text{个} 0},g_{-m},\cdots,g_{-2},g_{-1}] \end{gather}

al={flif l=0,1,⋯ ,nfl−Nif l=N−n,⋯ ,N−10otherwisea_l = \left\{\begin{aligned} &f_l&&\text{if }l=0,1,\cdots, n\\ &f_{l-N} &&\text{if }l=N-n,\cdots,N-1\\ &0&&\text{otherwise} \end{aligned}\right.

由于blb_l是"periodic extended"（参考example），因此bl=bl+N=bl−Nb_l = b_{l+N}=b_{l-N}

bl={gl+Nif l∈[−N+1,−N+m]glif l∈[−m,m]gl−Nif l∈[N−m,N−1]gl/gl−N/gl+N/0if l∈[−N+m+1,−m]∪[m+1,N−m−1]b_l = \left\{\begin{aligned} &g_{l+N}&&\text{if }l\in[-N+1,-N+m]\\ &g_l&&\text{if }l\in[-m,m]\\ &g_{l-N} &&\text{if }l\in[N-m,N-1]\\ &g_l/g_{l-N}/g_{l+N}/0&&\text{if } l\in[-N+m+1,-m]\cup[m+1,N-m-1] \end{aligned}\right.

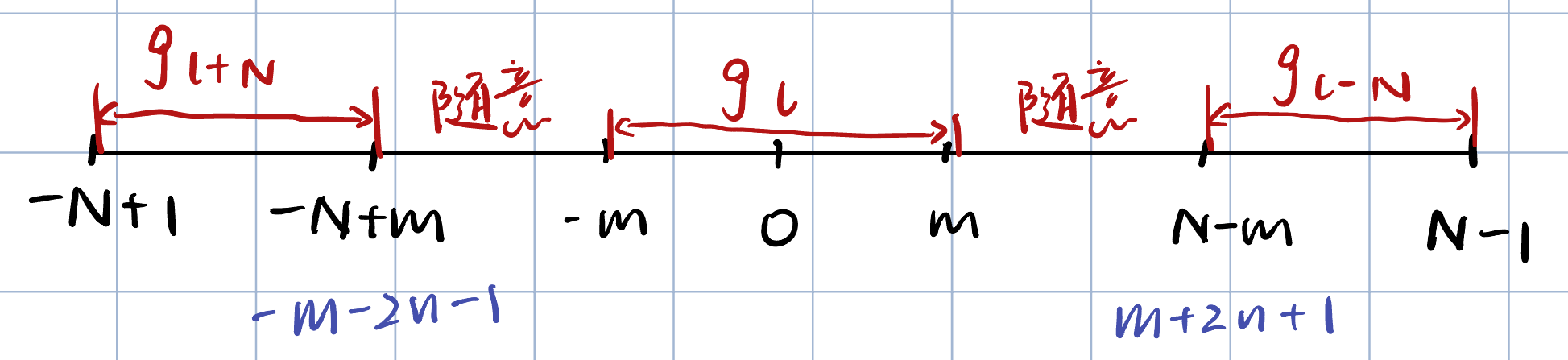
循环卷积 b

[g1,⋯ ,gm,0,⋯ ,0,⋯g−m,⋯ ,g−2,g−1,∣g0,g1,⋯ ,gm,0,⋯ ,0,g−m,⋯ ,g−2,g−1][g_1,\cdots,g_m,0,\cdots,0,\cdots g_{-m},\cdots,g_{-2},g_{-1},|g_0,g_1,\cdots,g_m,0,\cdots,0,g_{-m},\cdots,g_{-2},g_{-1}]

其中 l∈[−N+1,−m−1]l\in[-N+1,-m-1]的部分有：bl=bl+N=gl+Nb_l=b_{l+N}=g_{l+N}

对于 l∈[−m,−1]l\in[-m,-1]的部分有：bl=bl+N=glb_l=b_{l+N}=g_l

对于 l∈[0,N−m−1]l\in[0,N-m-1]的部分有：bl=glb_l = g_l

对于 l∈[N−m,N−1]l\in[N-m,N-1]的部分有：bl=gl−Nb_l=g_{l-N}

注意到，对于00，其既可以等于gl+Ng_{l+N}，也可以等于gl−Ng_{l-N}，也可以等于glg_l，因为都超出了[−m,m][-m,m]的范围，glg_l自动取0

(a⊛b)k=∑l=0N−1albk−l=∑l=0nalbl−k+∑l=N−nN−1albl−k(a\circledast b)_k = \sum_{l=0}^{N-1}a_lb_{k-l}=\sum_{l=0}^na_lb_{l-k}+\sum_{l=N-n}^{N-1}a_lb_{l-k}

对于k∈[0,m+n]k\in[0,m+n]

∑l=0nalbk−l=∑l=0nflgk−lk−l∈[−n,m+n]∑l=N−nN−1albk−l=∑l=N−nN−1fl−Ngk−l+Nk−l∈[−N+1,−m−1]=∑l=N−nN−1fl−Ngk−(l−N)=∑l=−n−1flgk−l\begin{align} \sum_{l=0}^{n}a_lb_{k-l}&=\sum_{l=0}^{n}f_lg_{k-l} && k-l\in[-n,m+n]\\ \sum_{l=N-n}^{N-1}a_lb_{k-l}&=\sum_{l=N-n}^{N-1}f_{l-N}g_{k-l+N} && k-l\in[-N+1,-m-1]\\ &=\sum_{l=N-n}^{N-1}f_{l-N}g_{k-(l-N)}\\ &=\sum_{l=-n}^{-1}f_{l}g_{k-l}\\ \end{align}

因此，

(a⊛b)k=∑l=0nalbl−k+∑l=N−nN−1albl−k=∑−nnflgk−l=(f∗g)k(a\circledast b)_k = \sum_{l=0}^na_lb_{l-k}+\sum_{l=N-n}^{N-1}a_lb_{l-k} = \sum_{-n}^nf_lg_{k-l} = (f*g)_k

对于k∈[m+n+1,N−1]k\in[m+n+1,N-1]

∑l=0nalbk−l=∑l=0nflgk−l−Nk−l∈[m+1,N−1]=∑l=0nflg(k−N)−l∑l=N−nN−1albk−l=∑l=N−nN−1fl−Ngk−lk−l∈[−m−n+1,n−1]=l−N→l~∑l~=−n−1fl~g(k−N)−l~\begin{align} \sum_{l=0}^{n}a_lb_{k-l}&=\sum_{l=0}^{n}f_lg_{k-l-N}&& k-l\in[m+1,N-1]\\ &=\sum_{l=0}^{n}f_lg_{(k-N)-l}\\ \sum_{l=N-n}^{N-1}a_lb_{k-l}&=\sum_{l=N-n}^{N-1}f_{l-N}g_{k-l} && k-l\in[-m-n+1,n-1]\\ &\overset{l-N\rightarrow \tilde l}{=}\sum_{\tilde l=-n}^{-1}f_{\tilde l}g_{(k-N)-\tilde l}\\ \end{align}

因此

(a⊛b)k=∑l=0nalbl−k+∑l=N−nN−1albl−k=∑−nnflg(k−N)−l=(f∗g)k−N(a\circledast b)_k = \sum_{l=0}^na_lb_{l-k}+\sum_{l=N-n}^{N-1}a_lb_{l-k} = \sum_{-n}^nf_lg_{(k-N)-l} = (f*g)_{k-N}

合并后：

(f∗g)=[(f∗g)−m−n,⋯ ,(f∗g)−1,(f∗g)0,(f∗g)1,⋯ ,(f∗g)m+n]⊤=[(a⊛b)m+n+1,⋯ ,(a⊛b)N−1,(a⊛b)0,(a⊛b)1,⋯ ,(a⊛b)m+n]⊤\begin{gather} (f*g) = [(f*g)_{-m-n},\cdots,(f*g)_{-1},(f*g)_{0},(f*g)_{1},\cdots,(f*g)_{m+n}]^\top\\ =[(a\circledast b)_{m+n+1},\cdots,(a\circledast b)_{N-1},(a\circledast b)_{0},(a\circledast b)_{1},\cdots,(a\circledast b)_{m+n}]^\top \end{gather}

证毕。